Graniastosłupy. Trudne. Gienek: W prostopadłościanie ABCDA'B'C'D' długość krawędzi AA' równa jest sumie długości krawędzi AB i AD. Punkt M jest rzutem prostokątnym wierzchołka B na przekątna AC podstawy ABCD. Wykaż, że MB' = MB + DB. Wiem, że w podstawie mam dwa trójkąty podobne prostokątne, ale nie wiem jak dalej ruszyć. Pomocy! :<

Panko: Widac twierdzenie o trzech prostych prostopadłych: prosta zawierająca MB^{`</sup> jest prostopadła do prostej zawierającej przekątną AC: stąd IMB<sup>`}I² = IMBI² +IBB^`I² Dalej to już z górki.

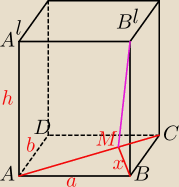
Bizon: h=|AA'|=|BB'|=a+b Twierdzenie podawane przez Panko to oczywista oczywistość x=|MB| policzysz z podobieństwa trójkątów ABC i BCM

Panko: dla oznaczeń jak u Bizona : 1^◯ IAMI =p I MCI =q wtedy p= a²/√a²+b² q= b²/√a²+b² wtedy ab=(p+q)*√pq ( fizycznie licząc p+q oraz pq ) 2^◯ Oznaczam h₁= IMB^`I wtedy h₁² =x² +(a+b)² z założenia czyli h₁² = x² +(a² +b²) + 2ab ale x²=pq stąd 3^◯ h₁² = pq +(a² +b²) + 2ab 4^◯ Ma być : h₁= x+ IACI bo IACI=IDBI stąd ma być h₁²=(√pq +p+q)² =pq+2(p+q)√pq +(p+q)²)= pq+2(p+q)√pq +(a²+b²)=pq+2ab + (a²+b²) na mocy 1^◯. A tyle wynosi h₁² obliczone w 3^◯ . Finito

Gienek: dzieki, teraz rozumiem