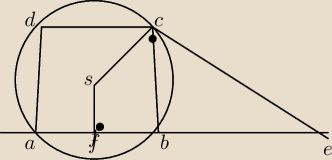
Pole czworokąta kropki1: Podstawy trapezu równoramiennego mają długość AB=8 cm DC=4cm. Na tym trapezie opisano okrąg. Styczna do okręgu w punkcie C przecina prostą AB w punkcie E. Wiadomo że CE=6√5 cm oraz pole trapezu ABCD jest o 6 większe od pola trójkąta BEC. Wyznacz promień okręgu opisanego na trapezie ABCD. Pabcd=Pbec − 6 Z twierdzenia o stycznej i siecznej wiemy, że: EC²=AE*BE 180=8x+x² Δ=784 √Δ= 28 x=10 EB=10 i wysokości są takie same ((8+4)h)/2 = (6√5h)/2 − 6 12h=6√5h − 12 −1,41h=−12 h=8,5 i co dalej ? jak wyznaczyć ten promień. Proszę o pomoc

mindfloer: Podstawiłeś zły bok trójkąta, bo wysokość h należy do boku |BC|, ponadto jeżeli pole trapezu jest o 6 cm² większe to: ((8+4)h)/2 = h*10*0,5 + 6 6h = 5h+6 h=6 (cm) Pbec = h*|bc|*0,5 = r*6√5*0,5 60=r*6√5 r=10/√5 r=2√5 (cm)

xvxvx: dlaczego Pbec = h*bc*0,5, przeciez to nieprawda...

Qulka: tam wstawił be a nie bc ... pewnie literówka