Podobieństwo trójkątów Radek: Ze środka przyprostokątnej BC trójkąta prostokątnego ABC poprowadzono odcinek DE prostopadły do przeciwprostokątnej. Wykaż, że trójkąty ABC i DBE są podobne oraz oblicz długości odcinków DE i BE, jeśli |BC|=8cm oraz |AC|=6 cm Jak można udowodnić że są podobne ? A w obliczeniu długości boków DE i BE zrobiłem tak i nie wiem do czego to przyrównać ? ⁶_|ED|= ? ⁸_|BE|=? Dziękuje za pomoc

Radek: Pomoże ktoś ?

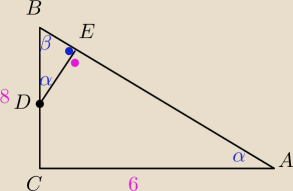
Mila: ΔBDE∼ΔABC cecha kkk DB=4 AB²=6²+8² AB=10

DB		AB
	=		⇔...
BE		BC

BD		AB
	=		⇔...
DE		AC

Radek: dziękuje bardzo wyszło 3,2 i 2,4. Te podobieństwo czytamy tak że DB jest podobny do AB BE jest podobny do BC ?

Mila: Nie bardzo wiem o co Ci chodzi. Odcinki zawsze są podobne do siebie, a Δ nie Proporcję

DB		AB
	=		czytamy tak:
BE		BC

DB tak się ma do BE jak AB do BC Układając proporcje kierujesz się tym jak położone są boki obu trójkątów− naprzeciw równych kątów. DB jest przeciwprostokątną w małym ΔDBE, BE jest przyprostokątną naprzeciw kąta α, tak samo AB to przeciwprostokatna w dużym ΔABC i przyprostokątna BC leży naprzeciw kąta ostrego α.

Radek: Bo zauważyłem że w liczniku są przyprostokątne. Czyli że DB jest podobne do AB ?

Mila: To są przeciwprostokątne.

Radek: A takie proporcje dobrze ułożyłem ^ED _BE = ^AC _BC Dziwnie się wyświetla to zapiszę tak ED/BE=AC/BC ?