nierówności kwadratowe z parametrem
Blondi: Dla jakich wartości parametru k równanie x2−(k+1)x+1,2k=0 ma dwa rozwiązania, z których jedno
jest równe sinusowi, a drugie cosinusowi tego samego kąta ostrego?
Skorzystać ze wzorów Viete'a.
2 gru 14:59
Bizon:
Δ≥0 ⇒ (k+1)
2−4,8k≥0 x
2−2,4k+1≥0 ... wnioski ...
x
1+x
2=sinα+cosα=k+1
...≤sinα+cosα≤... i do dzieła −
2 gru 15:10
Aga1.: x12+x22=1
2 gru 15:10
Bizon: ... chyba nie ...bo dla każdego kąta zachodzi sin2+cos2=1
2 gru 15:16
Bizon:
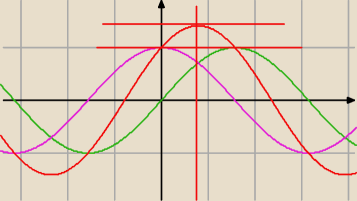
2 gru 15:21
2 gru 15:24
Blondi: Początek mam taki:
a≥0
sin2α+cos2α=1
x1+x2=1
x1+x2>0
x1*x2>0
później policzyłam deltę i k mi wyszło, że należy do przedziału (−∞ ; [ 7−2√6 ]:5 ) suma < [
7+2√6 ]:5 ; +∞)
i teraz nie wiem jak dalej to policzyć
Wzory Viete'a to:
x1+x2=−b/a
x1*x2=c/a
2 gru 15:53
Blondi: (−∞ ; [ 7−2√6 ]:5 ) suma ( [ 7+2√6 ]:5 ; +∞)
2 gru 15:54
Bizon:
... przecież napisałem Ci ....
2 gru 16:00
Tess: A skąd się wzięło, że 1<k+1<
√2 ?
(Dla wyjaśnienia − jeszcze nie miałam wykresów sinx i cosx)
7 gru 14:58