10 punktów, cieciwy strudzony_pal: Wszystkie sposoby zawodzą Na okręgu zaznaczono 10 punktów. a)Ile cięciw można poprowadzić w tym okręgu? b)Ile można utworzyć trójkątów, łączący odcinkami 3 jego punkty? odp. 45 i 120

strudzony_pal: pmc, pls.

Janek191: Zadanie jest już zrobione

strudzony_pal: Wiem, dzięki. Przepraszam za repost.

Saizou : z jednego punktu może wychodzić 9 cięciw, a punktów mamy 10 czyli 9*10=90, ale liczymy dwa razy cięciwy np. AB, BA a to bez różnicy dlatego trzeba podzielić przez 2 i uzyskamy 45

nic niemożliwego: (9*10)/2−= 45 bo z każdego punktu można poprowadzić 9 cięciw i każda ma jedna jest wspólna dla cięciwy tak jakby poprowadzonej od drugiego punktu

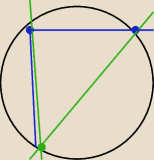
nic niemożliwego: W skład naszego trójkąta wchodzą dwie cięciwy i jedna cieciwa poprowadzona przez punkty niebieski i zielony. Więc za pomocą cięciwy możemy wykonać 10−2 = 8 trójkątów. Więc trójkątów będzie (45*8)/3 bo w jednym trójkącie zawierają się już trzy cięciwy/ (45*8)/3 = 120

Mila: Każde 3 różne punkty leżące na okręgu są niewspółliniowe. Liczbę Δ liczymy tak:

10 3		10!		8*9*10
	=		=		=4*3*10=120
		3!*7!		6