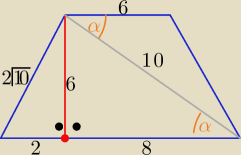
sernik: W trapezie równoramiennym podstawy maja długość 10 i 6, a ramię ma długość 2√10. Oblicz cosinus kąta ostrego między przekątną a podstawą. Proszę o pomoc

norka:

Godzio: d − przekątna a,b − odpowiednio krótsza i dłuższa przekątna c − ramie h − wysokość x − odcinek między wierzchołkiem dolnej podstawy, a spodkiem bliższej wysokości

	b − a
x =
	2

(b − x)² + h² = d² h² + x² = c² − ⇒ h = ... −−−−−−−−−−−−−−−−−−−− (b − x)² − x² = d² − c² ⇒ d = ...

	h
cosα =
	d

pigor: ..., czyli Δ równoramienny, więc długości rzutów prostokątnych jego ramion r na dłuższą podstawę r'= ¹₂(10−6)=2, więc h²=(2√10)²−2²=36 ⇒ h= 6=2+4 − długość wysokości trapezu równa zarazem długości rzutu prostokątnego przekątnej trapezu na dłuższą podstawę, czyli cos45^o=¹₂√2− szukany cosinus kąta. ...

Godzio: A ja walnąłem głupotę

	b − x
cosα =
	d

gucio: Ejj pigor ? ........ ( sprawdź co piszesz

gucio:

	8		4
cosα=		=
	10		5

bezendu: A gdzie Maja ? ?

pigor: .., przepraszam