geometria
madz,:
Bardzo proszę o pomoc

Dane są równania prostych k: 5x−2y−11=0 oraz l: x+2y+5=0, w których zawierają się dwa boki
równoległoboku. Punkt S (0 i 0,5) jest środkiem symetrii tego równoległoboku. Znajdź równania
prostych, w których zawierają sie pozostałe boki równoległoboku.
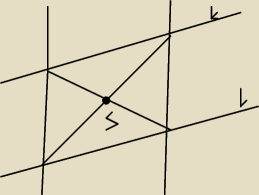
Naszkicowałam rysunek ale nie wiem czy coś pomoże

13 paź 22:30
Andrzej: zaznaczyłaś nie te proste co trzeba... Ty zaznaczyłaś proste równoległe, natomiast z równań
prostych k i l widać że nie są równoległe.
Zaraz napiszę szkic rozwiązania.
13 paź 22:37
Andrzej: 1. Znajdujemy punkt przecięcia prostych k i l −> niech nazywa się A.
2. znajdujemy wektor AS, dodajemy go do punktu S i otrzymujemy przeciwległy wierzchołek, czyli
punkt C.
3. Piszemy równania prostych równoległych do k i l przechodzących przez C − to będą szukane
proste.
Jeśli nie umiesz zrobić którejś z tych rzeczy napisz, pomogę.
13 paź 22:40
Andrzej: Dodam jeszcze że przy tym szczególnym położeniu punktu S (leży na osi OY) można zadanie
rozwiązać sprytnie w pamięci

13 paź 22:56
madz,: ten rysunek dla pomocy naszkicowała nam profesor

wiec nie wiem dlaczego jest zły.
13 paź 23:10
Andrzej: profesor też człowiek, może się pomylić
13 paź 23:37
madz,: oczywiście

13 paź 23:37
madz,: muszę przyznać, że kompletnie zgłupiałam nie wiem jak to zrobić
13 paź 23:45
Andrzej: Słonko... nie umiesz znaleźć punktu wspólnego prostych k i l ? Trzeba rozwiązać układ ich
równań:
5x − 2y = 11
x + 2y = −5
dodajemy stronami i wychodzi 6x = 6 czyli x = 1
a potem y = −3
Wierzchołek A ma współrzędne (1, −3)
13 paź 23:51
Andrzej: teraz wektor AS = [0 − 1, 0.5 − (−3)] = [−1; 3.5]
Dodajemy ten wektor do punktu S otrzymując przeciwległy wierzchołek C:
C = (0; 0.5) + [−1; 3.5] = (−1; 4)
teraz trzeba napisać równania prostych
równoległej do 5x −2y −11 = 0 przechodzącej przez (−1, 4)
i równoległej do x +2y + 5 = 0 przechodzącej przez (−1, 4)
13 paź 23:55
madz,: a na rysunku jak to będzie wyglądało?
14 paź 00:05
Andrzej: Sorki, ale nie podejmuję się tu zrobić rysunku... wpadnij do mnie to sobie porysujemy

14 paź 00:12
madz,: z miłą chęcią, ale trochę za późno

14 paź 00:19
Andrzej: ale dokończyłaś zadanko ?
powinno wyjść
5x − 2y + 13 = 0 i
x + 2y − 7 = 0
14 paź 00:21
madz,: nakieruj mnie chociaż czy strasznie źle jest w powyższym rysunku? heh
14 paź 00:21
madz,: tak tyle mi wyszło.
14 paź 00:22
Andrzej: w powyższym rysunku jest źle tylko to, że k i l są równoległe
14 paź 00:27
AROB:
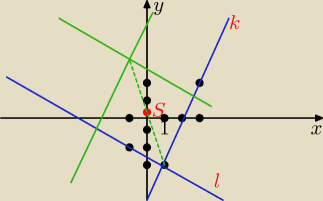
14 paź 00:28
14 paź 00:29
AROB: 
Żal mi się Ciebie zrobiło.
14 paź 00:31
madz,: wiesz, mi samej siebie żal nawet hehe

14 paź 00:32
AROB: 
Dobranoc. Powodzenia!
14 paź 00:41
madz,: Dobranoc, dzięki

14 paź 00:43
Bogdan:
| | 1 | |
A = (1, −3), S = (0, |
| ), C = (xc, yc), |
| | 2 | |
| | 1 + xc | | 1 | | −3 + yc | |
0 = |
| ⇒ xc = −1, |
| = |
| ⇒ yc = 4 |
| | 2 | | 2 | | 2 | |
C = (−1, 4)
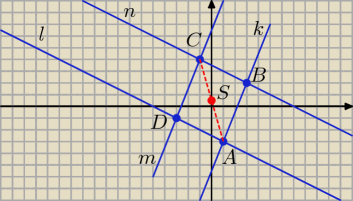
Przez punkt C prowadzimy prostą m równoległą do prostej k oraz prostą n równoległą
do prostej l.
14 paź 00:48
Bogdan:
O!

Już zrobiony rysunek, spóźniłem się

14 paź 00:50
madz,: ale również bardzo bardzo bardzo dziekuje za pomoc

14 paź 00:56
madz,: Bogdanie, czy możesz mi jednak wytłumaczyć jak rozwiązać to
Andrzej: teraz wektor AS = [0 − 1, 0.5 − (−3)] = [−1; 3.5] Dodajemy ten wektor do punktu S
otrzymując przeciwległy wierzchołek C: C = (0; 0.5) + [−1; 3.5] = (−1; 4) teraz trzeba napisać
równania prostych równoległej do 5x −2y −11 = 0 przechodzącej przez (−1, 4) i równoległej do x
+2y + 5 = 0 przechodzącej przez (−1, 4)
aby otrzymać
5x − 2y + 13 = 0 i x + 2y − 7 = 0
bo jednak pokręciłam coś źle mi wyszło:(
14 paź 00:58
Bogdan:
Uważam, że Andrzej wszystko klarownie wyjaśnił, pozostają więc tylko rachunki.
Proste są równoległe wtedy, gdy mają równe współczynniki kierunkowe.
| | 5 | |
Prosta m i prosta k mają współczynnik kierunkowy a1 = |
| . |
| | 2 | |
| | 1 | |
Prosta n i prosta l mają współczynnik kierunkowy a2 = − |
| . |
| | 2 | |
Proste m i n przechodzą przez punkt C = (−1, 4).
Jeśli dany jest współczynnik kierunkowy prostej a i punkt P(x
P,y
P), przez który ta
prosta przechodzi, to jej równanie wyraża się wzorem: y = a(x − x
P) + y
P
14 paź 01:11
madz,: dzięki
14 paź 01:14
 Bardzo proszę o pomoc
Bardzo proszę o pomoc Dane są równania prostych k: 5x−2y−11=0 oraz l: x+2y+5=0, w których zawierają się dwa boki
równoległoboku. Punkt S (0 i 0,5) jest środkiem symetrii tego równoległoboku. Znajdź równania
prostych, w których zawierają sie pozostałe boki równoległoboku.
Naszkicowałam rysunek ale nie wiem czy coś pomoże
Dane są równania prostych k: 5x−2y−11=0 oraz l: x+2y+5=0, w których zawierają się dwa boki
równoległoboku. Punkt S (0 i 0,5) jest środkiem symetrii tego równoległoboku. Znajdź równania
prostych, w których zawierają sie pozostałe boki równoległoboku.
Naszkicowałam rysunek ale nie wiem czy coś pomoże 

 wiec nie wiem dlaczego jest zły.
wiec nie wiem dlaczego jest zły.







 Żal mi się Ciebie zrobiło.
Żal mi się Ciebie zrobiło.

 Dobranoc. Powodzenia!
Dobranoc. Powodzenia!


 Już zrobiony rysunek, spóźniłem się
Już zrobiony rysunek, spóźniłem się 
