Przekształcananie wykresu funkcji
Kamix: Witam

Pomóżcie mi zapisać odpowiednia przekształcenia by móc narysować podaną funkcję:
f(x)=−2
x+1+2 dla x≤0
−|x−4|+4 dla x>0
Bardzo proszę krok po kroku o opisanie przekształceń
1 gru 16:31
bezendu:
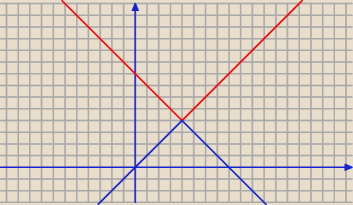
Coś mi tu pachnie zadaniem z matury

f(x)=−2
x v
→[−1,2]
f(x)=|x−4| o 4 jednostki do góry a potem to niebieskie trzeba zrobić

1 gru 16:36
bezendu:
oczywiście ja nie uwzględniałem tutaj przedziałów !
1 gru 16:37
zombi: Oho matura powrót!
1 gru 16:37
Kamix: Maturalne zadanko i nie wiedziałem jak to narysować ; /
1 gru 16:40
bezendu:
Wiemy, że maturalne, bo też pisaliśmy

1 gru 16:41
Kamix: I jak poszło?
1 gru 16:45
bezendu:
Średnio

A Tobie ?
1 gru 16:46
Kamix: Właśnie bardzo średnio, aż się boję gdy Pani odda. Chociaż pocieszam się, że nie mieliśmy
jeszcze stereometrii ani prawdopodobieństwa, Pani tych zadań nie będzie brać pod uwagę, czyli
2 zadania odpadną... Ale mam nadzieję, że oficjalna taka trudna nie będzie ; //
1 gru 16:47
Kamix: Ej głupi jestem, ale jak narysować wykres |x−4|?
1 gru 16:59
Radek:
|x| to wiesz ?
|x−4| przesunięty o 4 jednostki w prawo
1 gru 17:01
Kamix: A faktycznie, sorka, ale troszkę w szoku jestem po tej maturze

1 gru 17:02
Kamix: A teraz pytanie troszkę z innej beczki. Jak mam wielomian: W(x)=2x3−6x+4, to jak z niego
obliczyć W(x+1)=?
1 gru 17:10
Radek:
2(x+1)
3−6(x+1)+4 i tam była nierówność

1 gru 17:11
Kamix: o widzisz

A Tobie Radek jak poszło?

1 gru 17:11
Radek:
Nie zrobiłem:trygonometrii, planimetrii i prawdopodobieństwa

1 gru 17:14
Kamix: Czy tylko ja mam takie wrażenie, że ta matura była trudna?
1 gru 17:21
Radek:
Tak !
1 gru 17:22
Mila:
W maju są trudniejsze. Ta wyjątkowo była przyjazna uczniom.
Bezendu, co źle zrobiłeś?
Do maja dużo czasu. Nauczycie się.
1 gru 17:34
bezendu:
Ja już mam swoje wyniki, bo nasza Pani szybko sprawdziła i na librusie mam podane
podstawa 86%
roz 66% wiem, że na pewno zadanie z ostrosłupem źle bo nawet nie ruszyłem, pewnie coś jeszcze z
tym trójkątem nie tak. W środę będę wiedział dokładnie.
1 gru 17:38
zombi: Ja mam podstawa 96% a roszo mierze w 85+ jutro powiem jak roszo.
1 gru 17:40
bezendu:
Miałbym 96 jak bym zrobił ten graniastosłup. Zamknięte miałem wszystkie dobrze jak sprawdzałem,
wiec jeszcze odeszło za trapez

ehh
1 gru 17:42
zombi: Mi też za trapez poszło haha, że też tych kątów nie widziałem...
1 gru 17:42
Kamix: Mila, pocieszyłaś człowieka utrapionego...
1 gru 17:47
bezendu:
Na podstawie wgl nie było w otwartych zadania z prawdopodobieństwem i dowodu liczbowego.
1 gru 17:47
zombi: Ja wiem, że mam z roszo takie błędy:
| | 2 | |
−w zadaniu z logiem dałem odpowiedź (−1; − |
| ) zmiast > |
| | 3 | |
| | 13 | |
−prawdo błąd rachunkowy |
| |
| | 45 | |
−zadanie z kółkami przekombinowałem i nie doszedłem do ładnej odpowiedzi z tym sinusem.
1 gru 17:50
Mila:
Macie całkiem dobre wyniki, jak na tę porę roku szkolnego.
Zombi, Bezendu, gratuluję.
Będzie w lutym matura próbna, to wyniki Wam podskoczą do góry.
KamiX, i Radek, może nie będzie tak źle, jak sobie wyobrażacie.
1 gru 17:53
bezendu:
Ja po prostu muszę się zabrać za planimetrię ale to porządnie i analityczną

1 gru 17:54
zombi: To samo tutaj, plani, analityczna, to porażka jakaś xD dzięki Mila

1 gru 17:55
Mila:
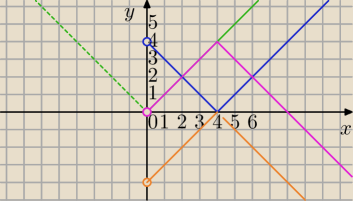
f(x)= −|x−4|+4 dla x>0
Po kolei:
1)
y=|x|→T[−4,0]→
y=|x−4| →S
OX→
y=−|x−4|→T[0,4]→
f(x)= −|x−4|+4 dla x>0
W następnym wpisie
|f(x)|
1 gru 18:05
Kamix: Dziękuję Mila, właśnie o takie przekształcenia krok po kroku mi chodziło ; ))
1 gru 18:11
Mila:
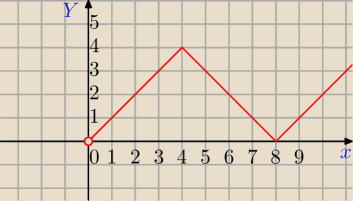
|f(x)|=|−|x−4|+4| dla x>0
1 gru 18:13
Kamix: W pierwszym przekształceniu po y=|x| nie powinna być translacja o wektor [4;0] zamiast [−4,0]?
1 gru 18:40
bezendu:
Powinno być tak jak mówisz.
1 gru 18:42
Kamix: Swoją drogą, dziękuję MILO STOKROTNIE

!
1 gru 18:44
Mila:
Naturalnie [4,0], nie wiem skąd mi ten minus wyskoczyl.
1 gru 18:51
 Pomóżcie mi zapisać odpowiednia przekształcenia by móc narysować podaną funkcję:
f(x)=−2x+1+2 dla x≤0
−|x−4|+4 dla x>0
Bardzo proszę krok po kroku o opisanie przekształceń
Pomóżcie mi zapisać odpowiednia przekształcenia by móc narysować podaną funkcję:
f(x)=−2x+1+2 dla x≤0
−|x−4|+4 dla x>0
Bardzo proszę krok po kroku o opisanie przekształceń
 Coś mi tu pachnie zadaniem z matury
Coś mi tu pachnie zadaniem z matury  f(x)=−2x v→[−1,2]
f(x)=|x−4| o 4 jednostki do góry a potem to niebieskie trzeba zrobić
f(x)=−2x v→[−1,2]
f(x)=|x−4| o 4 jednostki do góry a potem to niebieskie trzeba zrobić 

 A Tobie ?
A Tobie ?


 A Tobie Radek jak poszło?
A Tobie Radek jak poszło? 

 ehh
ehh


 f(x)= −|x−4|+4 dla x>0
Po kolei:
1) y=|x|→T[−4,0]→y=|x−4| →SOX→y=−|x−4|→T[0,4]→f(x)= −|x−4|+4 dla x>0
W następnym wpisie
|f(x)|
f(x)= −|x−4|+4 dla x>0
Po kolei:
1) y=|x|→T[−4,0]→y=|x−4| →SOX→y=−|x−4|→T[0,4]→f(x)= −|x−4|+4 dla x>0
W następnym wpisie
|f(x)|
 |f(x)|=|−|x−4|+4| dla x>0
|f(x)|=|−|x−4|+4| dla x>0
 !
!