wyznacz pole obszaru ograniczonego krzywymi
zosia: czy mógłby ktoś pomóc ?

wyznacz pole obszaru ograniczonego krzywymi:
y=sin x
dla x∊(o;π)
1 gru 16:12
zosia: jak się do tego zabrać ? ktoś pomoże ?
1 gru 16:26
Janek191:
y = sin x
−−−−−−−−−
sin x = 0,5
oraz
y = sin x
−−−−−−−−−−−
Pole jest równe
π x
4 x
1 x
2 π
P = ∫ sin x dx − ∫ sin x dx − [ ∫ sin x dx + ∫ 0,5 dx + ∫ sin x dx ] =
0 x
3 0 x
1 x
2
1 gru 16:31
Janek191:
y = sin x
−−−−−−−−−
sin x = 0,5
oraz
y = sin x
−−−−−−−−−−−
Pole jest równe
π x
4 x
1 x
2 π
P = ∫ sin x dx − ∫ sin x dx − [ ∫ sin x dx + ∫ 0,5 dx + ∫ sin x dx ] =
0 x
3 0 x
1 x
2
1 gru 16:31
Janek191:
Pomyłka − źle rozpisałem

1 gru 16:58
Janek191:
π x
4 x
1 x
2 π
| | √3 | |
P = ∫ sin x dx − ∫ sin x dx + ( x4 − x3)* |
| − [ ∫ sin x +0,5 ∫ dx + ∫ sin x dx ] = |
| | 2 | |
0 x
3 0 x
1 x
2
1 gru 17:19
Janek191:
π x
4 x
1 x
2 π
| | √3 | |
P = ∫ sin x dx − ∫ sin x dx + ( x4 − x3)* |
| − [ ∫ sin x +0,5 ∫ dx + ∫ sin x dx ] = |
| | 2 | |
0 x
3 0 x
1 x
2
1 gru 17:19
zosia: a czy mógłbyś powiedzieć co krok po kroku skąd się wzięło ? bo pogubiłam się w tym. byłabym
ogromnie wdzięczna.
1 gru 17:37
Janek191:
I całka to pole pod krzywą y = sin x , x ∊ < 0, π >
| | π | | 2 | |
II całka to pole pod krzywą y = sin x, x ∊ < |
| ; |
| π > |
| | 3 | | 3 | |
| | √3 | |
aby obliczyć pole nad prostą y = |
| muszę dodać pole prostokąta pod |
| | 2 | |
| | √3 | | π | | 2 | |
prostą y = |
| dla x ∊ < |
| ; |
| π > |
| | 2 | | 3 | | 3 | |
Całki w nawiasie dają razem pole pod kawałkami sinusoidy i prostej y = 0,5
1 gru 17:51
Janek191:
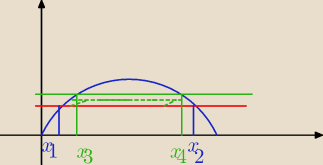
1 gru 18:02
zosia: | | √3 | | √2 | |
a dlaczego y= |
| ? czy nie powinno to być y= |
| |
| | 2 | | 2 | |
1 gru 18:57
Janek191:
Faktycznie − źle przepisałem

1 gru 22:26
 wyznacz pole obszaru ograniczonego krzywymi:
y=sin x
wyznacz pole obszaru ograniczonego krzywymi:
y=sin x


