parametry tadam: dla jakich wartości parametru a rozwiązanie układu jest parą liczb o różnych znakach? {ax−y=−2 {x+ay=7 W= a²+1 W_x=−2a+7 W_y=7a−2 a∊R − u. oznaczony x=−2a+7/a²+1 y=7a−2/a²+1 xy<0 (−2a+7/a²+1 )* (7a−2/a²+1)<0 −14a²+53a−14<0 Δ=2025 a₁=3,5 a₂=2/7 w odp. (−∞,−2/7)∪(7/2,∞) wytłumaczyłby mi ktoś dlaczego tak utworzono te przedziały?

tadam: chodzi mi o te przedziały z odp. bo nie wiem dlaczego mając a₁ i a₂ otrzymujemy taką odp.

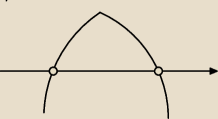
fdsf: zobacz jeśli masz −14a²+53a−14<0 oraz pierwiastki a₁=⁷₂ a₂=²₇ musisz narysować parabole oraz odczytać przedziały

help: to dlaczego w poprzednim przykładzie miałam: {2x−4y=a {−3x+4y=5 W=−4 W_x=4a+20 W_y=10+3a a∊R − u. oznaczony x=−5−a y=10+3a/−4 xy<0 12a²+100a+200<0 Δ=400 a₁=−5 a₂=−10/3 a∊(−5,−10/3) tak jak mi wyszło zgodnie z odp. a nie (−∞,−5)∪(−10/3,∞) ?

help: ?

fdsf: bo patrzysz na 1) jeśli liczba jest dodatnia przy a² to rysujesz wykres "uśmiechniętą" a jesli −a² to "smutna";. 2)jeśli >0 to liczby nad osią , jeśli <0 liczba pod osią.