równanie Radek: Mam takie równanie ax+a=x wyznacz wszystkie wartości parametru a dla których to równanie jest sprzeczne: ax+a=x ax−x=−a x(a−1)=−a a−1≠0

	−a
x=
	a−1

a=1 sprzeczność

Godzio: Ok

Grzech: wynik dobry, ale sam zapis średni jak dla mnie.

Piotr 10: ax+a=x ax−x+a=0 (a−1)*x+a=0 A=0 ⋀ B≠0 Ax+B=0 a−1=0 ⋀ a≠0 a=1 ⋀ a≠0 ODP: a=1 OK.

Radek: Godzio zapis ok ?

Radek: wykaż, że równanie ze zmienną x i parametrem a a²x+ax=1−x ma rozwiązanie dla dowolnej wartości parametru a ax²+ax+x=1 x(a²+a+1)=1

	1
x=
	a2+a+1

i teraz mam w mianowniku f.kwadratową parabola ramionami do góry Δ<0 więc nie ma miejsc zerowych ? o to chodzi ?

Saizou : nie możesz podzielić przez 'x', bo nie wiesz czy nie jest przypadkiem 0 (ewentualnie dzieląc przez 'x' musisz rozpatrzeć przypadek"co by było gdyby x=0")

Saizou : sorry nie patrz na mój post, bo widziałem tam ax² zamiast a²x

Radek: czyli ?

Saizou : a teraz do zadania, wystarczyło sprawdzić czy a²+a+1≠0 bo nie można dzielić przez 0, a skoro

	1
a2+a+1>0 to x=		ma rozwiązanie dla a∊R
	a2+a+1

Radek: a∊R napisałem wcześniej czemu ?

Piotr 10: a²x+ax=1−x a²x+ax+x −1 =0 (a²+a+1)*x − 1=0 A≠0 ∧ B∊R Ax+B=0 a²+a+1≠0 Δ_a<0 i ramiona skierowane do góry więc a²+a+1 >0 dla a∊R c.n.w

Radek: Piotr czemu Ty zapisujesz to w postaci funkcji liniowej ?

Saizou : bo Piotr korzysta z postaci ogólnej prostej

Piotr 10: Wynika to z wykresu funkcji liniowej Gdy mamy funkcję postaci ax+b=0 I a=0 i b=0 wtedy wykres funkcji nakłada się na oś OX, więc ma nieskończenie wiele rozwiązań II a≠0 i b∊R wtedy wykres funkcji przecina tylko raz oś OX, czyli ma jedno rozwiązanie III a=0 i b≠0, wtedy otrzymujemy funkcję stałą nad osią OX lub pod osią OX, czyli brak rozwiązań(bo nie przecina w ogóle osi OX)

Radek: to takie coś a²x−x=a+1 x(a²−1)=a+1 x(a−1)(a+1)=a+1 dla a=1 sprzeczność dla a=−1 tożsamość dla a≠−1 i a≠1 oznaczone ?

Radek: ?

Lemon: Ok

Radek: Dane jest równanie ze zmienną x i parametrami a,b: ax+2b=bx+2a Zbadaj ilość tego równania w zależności od a i b ax−bx=2a−2b x(a−b)=2(a−b) dla a=b tożsamość dla a≠b oznaczone ?

Mila: Dobrze. 1) a=1, to wtedy masz sytuację: x*0*2=2 sprzeczność, bo wychodzi 0=2 ( równanie sprzeczne) 2) a=−1, to wtedy masz : x*(−2)*0=0 niezależnie co podstawisz za x masz 0=0, równanie ma nieskończenie wiele rozwiązań. 3) a≠1 i a≠−1 równanie ma dokładnie jedno rozwiązanie ( oznaczone)

	a+1
x=		⇔
	(a−1)*(a+1)

	1
x=
	a−1

===========

Radek: Pani Milu a mogę sobie tak bezkarnie dzielić ? czy dopiero po wyznaczeniu dziedziny ?

Radek: ?

Mila: Po zaznaczeniu, że dzielnik różny od zera. W 3 przypadku masz podane: a≠1 i a≠−1 w drugim zadanku napisałeś: a≠b, wtedy możesz zapisać:

	2(a−b)
x=		⇔
	a−b

x=2

Radek: Dane jest równanie x³+px²+px+p²=0 z niewiadomą x. Wyznacz liczbę różnych rozwiązań tego równania w zależności od parametru p ? x³+px²+px+p²=0 x²(x+p)+p(x+p)=0 (x+p)(x²+p)=0 x=−p nie wiem ?

Eta: (x+p)(x²+p)=0 dla p=0 jedno rozwiązanie, bo x³=0 ⇒ dla p<0 x+p=0 −−1 rozwiązanie i x²+p =0 −− 2 rozwiązania ( r−m 3 rozwiązania) dla p>0 x+p =0 −− 1 rozw. i x²+p=0 −− sprzeczne w zb. R

Eta: "puk−puk" ?

Radek: Dobry wieczór Pani Eto zaraz przeanalizuję !

Eta: Hej zieloną ?możesz zjeść, ale czerwona Eta musi zostać! przynajmniej do maja 2014

Radek: Czemu do maja 2014 ? Ja mówiłem o

Eta: Napisałeś Eto

Mila: Znowu flirtujecie?

Radek: A tak jakoś Dane jest równanie px²+1=p z niewiadomą x i parametrem p∊R wyznacz liczbę rozwiązań tego równania w zależności od parametru p px²−p+1=0 dla p=0 jedno rozwiązanie dla p<o dwa rozwiązania dla p>0 brak rozwiązań ?

Eta: Witaj Mila ( czemu "smutny kolor" ? ) ...

Eta: Ejjj Raduś dla p=0 ...................... co otrzymasz? ( myśl troszkę

Mila: Witaj Eto! Komputer wysiadł, jestem na gościnnych występach.

Radek: Dla 1=0 sprzeczność czyli brak rozwiązań ! przepraszam

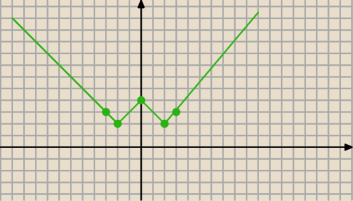
Radek: Dane jest równanie ||x|−2|+2=|p| z niewiadoma x. Wyznacz liczbę rozwiązań tego równania w zależności od parametru p. Narysuj wykres funkcji f(p) która przyjmuję dla danego p∊R wartość równą ilości rozwiązań powyższego równania. jak bym miał p to nie miałbym problemu ale tutaj mam |p| ?

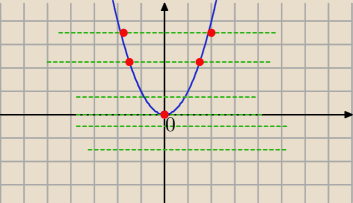
Eta: zobacz teraz graficznie: px²+1=p dla p≠0

	p−1
x2=
	p

	p −1
0 rozwiązań dla .........		<0 ⇒ p∊
	p

1 rozwiązanie dla .... 2 rozwiązania dla ... dokończ.........

Eta: "jakbym miał p ... a mam |p| to rozwiąż tak jak dla "p" tylko z modułem i rozwiąż .....

Eta: Np 2 rozwiązania dla |p|=2 lub |p| >4 i teraz rozwiąż .......

Radek: p∊(−∞,2) brak rozwiązań p∊{2} dwa rozwiązania p∊(2,4) cztery rozwiązania √4 trzy rozwiązania p∊(4,∞) dwa rozwiązania

Radek: p∊{4} trzy rozwiązania

Eta: popraw , i napisz jeszcze raz odpowiedzi np: trzy rozwiązania dla: 4<|p|<2⇒ |p|<2 i |p|>4 ⇒ p ........

Radek: To jest rozwiązanie dla p a nie |p|..

Radek: hmm ?

Radek: ?

Radek: