. Piotr 10: Oblicz, ile jest wszystkich możliwych liczb sześciocyfrowych, w których zapisie występują dokładnie dwie cyfry nieparzyste. Na pierwszym miejscu cyfra nieparzysta 5*5*5*5*5*5*5=5⁷ Na pierwszym miejscu cyfra parzysta

	5 3
4*		*5*5*5

	5 3
57+4*		*5*5*5=...

Hmm?

Piotr 10: W urnie jest 5 białych kul i 10 czarnych kul. Wyjmujemy jedną kulę, odkładamy, a następnie z pozostałych wyjmujemy dwie kule. Oblicz prawdopodobieństwo, że za drugim razem wyjmiemy dwie kule białe.

	15 1
C115=		=15

	14 2
C214=		=91

Ω=15*91=1365

	4 2		5 2
A=		+

?

Saizou : coś masz źle z tym co na pierwszym miejscu jest parzysta 4*C²₅*5²*5³

Saizou : a w tym drugim proponuje zrobić drzewko

Piotr 10: Nie umiem drzewek , czyli drugie zadanie źle ?

Saizou :

	187
drzewka nie są trudne, wynik to P(A)=
	462

Piotr 10: Czyli źle na pewno, bo A=16( u mnie) A mógłbyś mi wytłumaczyć te drzewka ?

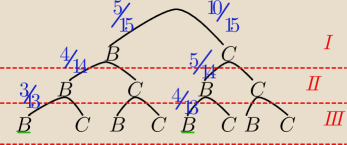
Saizou : na przykładzie tego zadania: −na początku możemy wylosować białą lub czarną kulę (czyli zaznaczam na drzewku możliwe wybory= I poziom drzewka) − następnie z każdej z opcji możemy wybrać 2 kule (czarną albo białą )=II poziom − i dalej mamy wyciągnąć 2 kulę (białą lub czarną )= III poziom i teraz należy rozpisać prawdopodobieństwo (ja rozpisze tylko dla zdarzeń sprzyjających, czyli na tych podkreślonych na zielono) i teraz na gałęzi mnożymy prawdopodobieństwa a między nimi się dodaje

	5		4		3		10		5		4		260
P(A)=		*		*		+		*		*		=
	15		14		13		15		14		13		2730

Piotr 10: Już patrzę

Saizou : tylko wynik mi się nie zgadza z operonem ale myślę że to błąd w druku

Piotr 10: A dobry jest ten zbiór zadań z Operonu? Arkusze maturalne itd ? Co sądzisz

Saizou : jak dla mnie to trochę zbyt typowy, zadania są schematyczne i trochę to razi, ale tak poza tym nawet dobry, choć czasami ich rozwiązania nie są na poziomie liceum np. twierdzenie o trzech ciągach

Piotr 10: Nie rozumiem dlaczego są trzy poziomy. Najpierw wyjmujemy jedną kulę, odkładamy ją i potem wyjmujemy dwie kule I nie wiem czemu w tym drzewku jest, że 2 razy wyjmujemy dwie kule

Saizou : a jak chcesz zaznaczyć że wyjmujesz 2 kule jednocześnie ? nie da się tego zrobić (bynajmniej ja nie umiem)

Piotr 10: A no tak, myślałem, że jednocześnie, ok. Napiszę zadanko, zrobię je drzewkiem u siebie na kartce i sprawdzisz wynik ok? Zapewne masz odpowiedź do tego zadanka, ok?

Saizou : ok

Piotr 10: W urnie I jest 5 białych kul i 7 czarnych kul, w urnie II są 2 białe kule i 3 czarne kule. Wyjmujemy dwie kule z I urny i dokładamy do II urny, a następnie z II urny wyjmujemy jedną kulę. Oblicz prawdopodobieństwo, że po dołożeniu kul wyjmiemy z II urny kulę czarną. Już je robię

Piotr 10: Chyba za trudno dla mnie , mogę prosić o pomoc ?

Saizou : to trzeba pierwszy poziom rozrysować (z pierwszej urny losujemy czarną lub białą) i powtarzamy tę czynność ..... a potem II urna

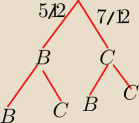
Piotr 10: Ta początkowa sytuacja, tak wygląda ?

Saizou : tak, na razie ok

Piotr 10: I co dalej?

Saizou : masz sytuację rozpisaną do momentu kiedy wyjmujemy 2 kule z urny I, teraz musisz jeszcze rozpisać możliwości z II urny

Piotr 10: Tylko nie wiem jak to będzie z tym dokładaniem kuli do II urny

Saizou : z urny II dla każdego przypadku możemy wylosować czarną lub białą kulę

Piotr 10: To wiem, tylko teraz chodzi mi o zapisanie tego prawdopodobieństwa nad kreseczkami

Saizou : ale jeszcze musisz rozpisać dla wybrania drugiej kuli z I urny a w urnie II ilość kul się zwiększyła o to co wylosowaliśmy

Piotr 10: Czyli I urna (prawdopodobieństwa nad kreseczkami) Zaczynając od lewej strony to 4/11 ; 7/11 ; 5/11 ; 6/11 OK?

Saizou : tak

Piotr 10: Dobra to teraz druga urna( po dołożeniu tych dwóch kul) I mam problem z zapisaniem tego prawdopodobieństwa

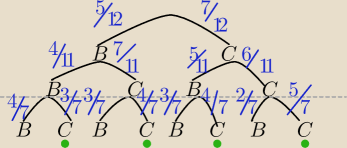
Saizou : no i teraz masz źle bo to trzeba dołączyć do każdego z wyborów 2 kuli z I urny

Piotr 10: Mógłbyś mi to rozpisać ?

Saizou :

Piotr 10: Ok to rozumiem, teraz jak to wymnożyć ?

Saizou : na gałęziach mnożysz a między nimi dodajesz

Piotr 10: Czyli tak

	5		4		3		5		7		4		7		5		4
P(A)=		*		*		+		*		*		+		*		*		+
	12		11		7		12		11		7		12		11		7

	7		6		5
+		*		*		=.. ? tak?
	12		11		7

Saizou : tak

Piotr 10: Uff, dobra teraz spróbuję samemu zrobić zadanie z tymi drzewami. Dzięki za pomoc . Będę pisał w razie czegoś

Saizou : jak będę jeszcze na forum to pomogę (jeśli będę umiał)

Piotr 10: Dzięki Tobie ogarnąłem te drzewka, zrobiłem samemu inne zadania i sobie poradziłem. Nawet zadanie z próbnej matury z Operonu później udało mi się zrobić . Dzięki jeszcze raz

Saizou : to się cieszę że Ci się udało to ogarnąć