oblicz djuuud: Obwód pewnego trójkąta jest równy 6 cm, a jeden z jego kątów ma miarę 60 stopni. Promień okręgu opisanego na tym trójkącie ma długość R= (2√3)/3 cm. wyznacz długości boków tego trójkąta tak aby jego pole było największe . oblicz pole trójkąta dla wyznaczonych boków.

djuuud: Come on!

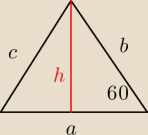
Janek191: α = 60^o

	2√3
R =
	3

Mamy

	√3
P = 0,5 a*b*sin 60o = 0,5 a*b*
	2

oraz

	a*b*c		a*b*c		3a*b*c
P =		=		=
	4 R		2√3   4*   3		8√3

zatem

	√3		3a*b*c
0,5 a*b*		=		/ : a*b
	2		8 √3

	√3		3 c
0,5		=		/ * 8√3
	2		8√3

6 = 3 c c = 2 −−−−−− a + b + c = 6 ⇒ a + b + 2 = 6 ⇒ a + b = 4 ⇒ b = 4 − a czyli

	√3
P = 0,5 a*b sin 60o = 0,5 a*(4 − a)*		= 0,25√3 a*( 4 − a)
	2

P( a) = − 0,25√3 a² + √3 a Funkcja P(a) posiada największą wartość, bo − 0,25 √3 < 0

	− √3
dla a = p =		= 2
	− 0,5 √3

Wtedy b = 4 − a = 4 − 2 = 2 Mamy zatem a = b = c = 2

	a2 √3		22 √3
PΔ =		=		= √3
	4		4

Odp. Jest to trójkąt równoboczny o polu P = √3 [j²} =======================================

djuuud: Dziękiiiiiiiiiiiiiii!