sprawdzcie jerey: dla jakich wartosci parametru a rownanie |x−1|=a²−4a−1 ma dwa dodatnie pierwiastki? moj tok rozumowania |x−1|=m jezeli ma 2 dodatnie pierwiastki to musza byc w 1 cwiartce wykresu. m>1 zatem a²−4a−1>1?

jerey: a²−4a−1<1 i a²−4a−1>0

bezendu: b=a²−4a−1 |x−1|=b x−1=b x−1=−b b+1>0 −b+1>0 a²−4a>0 i −a²+4a+2>0 cześć wspólna i koniec zadania

pigor: ..., , nie pospieszyłeś się za bardzo, może jednak warunki zadania są spełnione ⇔ 0< a²−4a−1< 1 , co ?

jerey: dobra pigor, doszedłem do tego co napisałes. dzieki

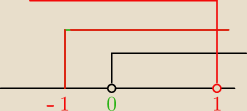
bezendu: dla jakich wartosci parametru a rownanie |x−1|=a²−4a−1 ma dwa dodatnie pierwiastki m=a²−4a−1 według Twoich oznaczeń |x−1|=m Żeby to miało dwa pierwiastki dodatnie to m>0 x−1=m x−1=−m x=m+1 x=−m+1 m+1>0 −m+1>0 m−1<0 m>−1 m<1 a²−4a>0 i −a²+4a+2>0 więc w niczym się nie pospieszyłem !

pigor: ... , moje pytanie nie było do ciebie kolego,

Radek:

bezendu: No i ok