Planimetria Forrest: Promień okręgu wpisanego w trójkąt prostokątny jest równy 2. Tangens jednego z kątów ostrych trójkąta wynosi 3/4. Oblicz odległość między wierzchołkiem kąta prostego, a punktem styczności okręgu z przeciwprostokątną. Kompletnie nie wiem jak to ruszyć, dzięki z góry za pomoc.

Forrest: Pomoże ktoś? Byłbym bardzo wdzięczny!

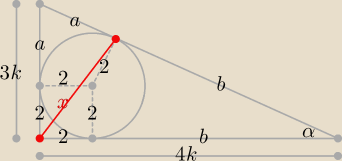
Bogdan: a = 3k − 2, b = 4k − 2, a + b = √9k² + 16k² = 5k ⇒ 3k − 2 + 4k − 2 = 5k ⇒ k = 2

	3
tgα =		⇒ cosα = ...
	4

Na podstawie twierdzenia kosinusów: x² = (4k)² + b² − 2*4k*b*cosα