. Piotr 10: Spośród wierzchołków trójkąta równobocznego o boku 6 i środków jego boków wybrano losowo 3 punkty. Oblicz prawdopodobieństwo, że wybrano punkty będące wierzchołkami trójkąta o polu

	9√3
równym		.
	2

Ω − zbiór 3−elementowych kombinacji zbioru 6−elementowego A − wybranie punktów będących wierzchołkami trójkąta o danym polu.

	6 3
IΩI=		=20

IAI=4

	1
P(A)=
	5

Jednak w kluczu jest, że IAI=6 Proszę o pomoc

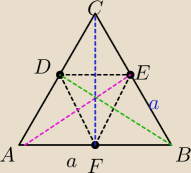
Hajtowy: Trójkąty o polu równym połowie ABC: ACF,ACE,BCF,BCD,ABE,ABD. D to środek AC, E to środek BC F to środek AB. No więc jest ich 6 Stąd też |A| = 6

-:): a Ω Twoi zdaniem dobrze ... czy każde trzy tworzą trójkąt ? (chyba, że specyficzny ... o polu równym 0)

Piotr 10: Nie wiem, dla mnie moje rozwiązanie wyglada dobrze

Hajtowy: |Ω| jest dobrze. |A|=6 −> wyjaśnienie wyżej.

	6		3
P(A)=		=
	20		10

Piotr 10: Zaraz zobaczę, odpocznę sobie, bo ten dział mnie denerwuje

Mila:

	62√3
PΔABC=		=9√3
	4

	9√3
PΔADF=
	4

	1		3√3		9√3
PABD=		*6*		=		takich Δ szukasz.
	2		2		2

|Ω|=liczba wyborów 3 punktów z 6. Sprzyjające wybory to wierzchołki 6 Δ.

Piotr 10: Ok dzięki