proszę :) Weronika: Dane są okręgi x² +y² +8x + 2y + 1 = 0 i (x − 2)² + (x − 2)² + (y − 7)² = m²b− 2m +1. Wyznacz m tak, aby te okręgi miały co najmniej jeden punkt wspólny.

-:): x²+8x+16−16+y²+2y+1−1+1=0 (x+4)²+(y+1)²=16 zatem pierwszy okrąg ma środek S₁=(−4,−1) W równaniu drugiego okręgu pewnie zdublowałaś te (x−2)² ?

Hajtowy: x² +y² +8x + 2y + 1 = 0 Bez żadnych wzorów skróconego mnożenia można to zrobić −2a=8 a=−4 −2b=2 b=−1 c=1 Mając tablice matematyczne przed sobą od razu widać, że środek okręgu S=(−4;−1)

Weronika: tak xD

Weronika: i bez tego b przy m

-:): ... jak kto woli Hajtowy

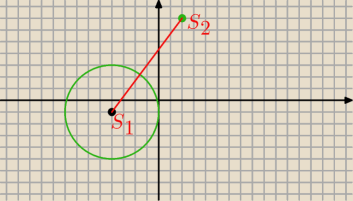
-:): ... i teraz układ nierówności

Gustlik: Są wzory na środek i promień okręgu, nie potrzeba się męczyć wzorami skróconego mnożenia: x²+y²+Ax+By+C=0

	A
a=−
	2

	B
b=−
	2

r=√a²+b²−C, gdy a²+b²−C>0 x² +y² +8x + 2y + 1 = 0

	8
a=−		=−4
	2

	2
b=−		=−1
	2

r=√(−4)²+(−1)²−1=4 S₁=(−4, −1), r₁=4 (x − 2)² + (y − 7)² = m²− 2m +1 x−2=0 ⇔ x=2 y−7=0 ⇔ y=7 S₂=(2, 7), r₂=√m²− 2m +1=√(m−1)²=|m−1|, m−1≠0 ⇔ m≠1 (aby nie był to punkt) Aby okręgi miały co najmniej jeden punkt wspólny, to: |r₁−r₂|≤|S₁S₂|≤r₁+r₂ S₁S₂^→=[2−(−4), 7−(−1)]=[6, 8] |S₁S₂|=√6²+8²=10 r₁+r₂=4+|m−1| |r₁−r₂|=|4−|m−1|| |4−|m−1||≤10≤4+|m−1| |4−|m−1||≤10 4−|m−1|≤10 i 4−|m−1|≥−10 −|m−1|≤6 i −|m−1|≥−14 |m−1|≥−6 ⇔ m€R i |m−1|≤14 m=1±14 m=−13 v m=15 m€<−13, 15> 10≤4+|m−1| 4+|m−1|≥10 |m−1|≥6 m=1±6 m=−5 v m=7 m€(−∞, −5>U<7, +∞) Część wspólna: Odp: m€<−13, −5>U<7, 15>