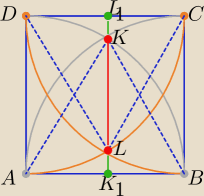
Dany jest kwadrat ABCD o boku a. Punkt K jest punktem wspólnym okręgów o(A,a) i kamczatka: Dany jest kwadrat ABCD o boku a. Punkt K jest punktem wspólnym okręgów o(A,a) i o(B,a), punkt L jest punktem wspólnym okręgów o(C,a) i o(D,a), przy czym oba punkty należą do kwadratu ABCD. Wyznacz odległość między punktami K i L. Jak powinien wyglądać rysunek ?

kamczatka: ?

kamczatka: ?

kamczatka: czyli nikt nie wie ?

Panko: ΔABK oraz ΔDLC są równoboczne o boku długości a ( warunki zadania) KK₁− wysokość ΔABK z wierzchołka K na bok AB analogicznie LL₁− wysokość ΔDLC z wierzchołka L na bok DC ILL₁I=IKK₁I=(a√3)/2 Ponieważ KL= KK₁∩LL₁ ( jako odcinki) to IKLI=IKK₁I +ILL₁I −IKLI stąd 2IKLI = 2*(a√3)/2 stąd IKLI= (a√3)/2 gdzie I KL I −−−długość odcinka KL

kamczatka: nic nie ogarniam z tego

Eta:

Eta: A teraz ?

Radek: Kamczatka śpi

kamczatka: to zadanie mnie przerasta o(A,a) czyli środek tego okręgu to A a na rysunku jest jako wierzchołek to nie rozumiem.

Eta: Okręgi mają środki w wierzchołkach kwadratu i promienie długości r= a Czego tu jeszcze nie rozumiesz? teraz zobacz rozwiązanie Pańko ( specjalnie dałam Ci takie oznaczenia, jakie podał