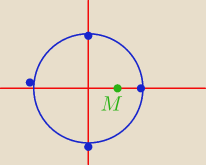
geometria na płaszczyźnie Maniek: Równaniem miejsca geometrycznego punktów równo odległych od okręgu o równaniu x² +y²=100 i punktu M=(6,0) jest: a) okrąg o równaniu (x−6)²+y²=100

	x2		y2
b) hiperbola o równaniu		−		=1
	25		16

	(x−3)2
c) elipsa o równaniu		+{y2}{16}=1
	25

	x2		y2
d) elipsa o równaniu		+		=1
	25		16

Może być więcej niż jedna odpowiedź. Można mi wytłumaczyć na czym wgl ma polegać to zadanie? Niezbyt rozumiem polecenie. O co z tym chodzi?

-:):

Kejt: a to nie chodzi o poprzekształcanie tych wyrażeń tak aby dostać równanie okręgu? (takie jak jest w a)

Kejt: dobra.. nieważne.. mój mózg już się do niczego nie nadaje

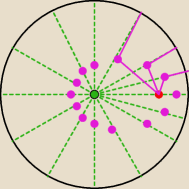
-:): ... nasz punkt M Wyznaczyć trzeba miejsce geometryczne punktów równoodległych od okręgu i danego punktu. Mówiąc inaczej wyznaczyć wszystkie takie punkty, których odległości od okręgu i M są równe. (jak na rysunku) Mamy współrzędne punktu M i równanie okręgu ... elipsa do sprawdzenia −

Maniek:

	(x−3)2		y2
Będzie to elipsa z odpowiedzi c)		+		=1?
	25		16

MQ: Tak

Maniek: Dziena

Panko: Na szybko: (x−6)²+y²=(x−10cost)² +(y−10sint)² gdzie x=10cost, y=10sint; x²+y²−12x+36=x²+y²+100(sin²t+cos²t)−20(xcost+ysint) −12x+36=100−2(x²+y²) x²+y²−6x−32=0 −−−−−−locus zadaniowe

MQ: Walnąłeś się Panko w obliczeniach.

Panko: Gdzie przekręciłem ?

MQ: Dwa ostatnie wiersze są źle.

Panko: Widzę ,że suma odległości od punktu M i od (0,0) musi być stała (10−d) +d czyli to powinna być elipsa.

MQ: I jest.

Panko: Ale na Eulera Algebra się nie myli, tylko ja . Gdzie popsułem ?

Panko: Tak jest to elipsa o ogniskach F₁=(0,0) F₂=(6,0) 2a=10; 2c=6; wtedy b²=a²−c²=16 (x−3)²/a² +y²/b² =1 (x−3)²/25+y²/16= 1