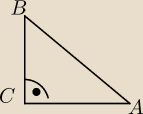
PLANIMETRIA Kasia: Dany jest trojkat prostokatny abc w ktorym ∡BCA=90(stopni, |AB|=2√5 i |BC|=4 mozecie mi narysowac ten trojkat bo zle go rysuje

5-latek: Mamsz dobrze narysowane Teraz oznacz boki AB=2√5 i zauwqaz ze jest to przeciwprostokatna tego trojkata oznacz bok BC =4 i jest to jedna z przyprostokatnych tego trojkata Natomiast bok CA wylicz ztwierdzenia PItagorasa |aB|²=|BC|²+|AC|² to |AC|²=|AB|²−|BC|²=(2√5)²−4²= licz

Kasia: 2√5−4?

Kasia: 20−16=6

Kasia: sory 20−16=4

5-latek: Skad ja wiedzialem ze wlasnie z liczeniem bedzie problem Nie przeciez zdodnie z ewzorem (a*b)²=a²*b² to (2√5)²=2²*(√5)²=4*5= ile 4²=16 wiec to teraz odejmnij od siebie i napisz ile jest rowne AC

5-latek: No to wyliczylas ze |AC|²=4 to |AC|= ile

Kasia: zapomnialam 2

5-latek: Dobrze w tym przypadku AC=2 Ale tez jest drugie rozwiazanie ze |AC|=−2 bo (−2)² tez da 4 ale ze bok trojkata nie moze miec wartosci ujemnej wiec rozwiazanie to |AC|=2 . OK?

Kasia: OK dzieki

5-latek: