Okrąg bezendu: Okrąg o równaniu x²−6x+y²−2y+2=0 i prosta x+3y+2= przecinają się w punktach A, B wyznacz długość cięciwy AB. Proszę o sprawdzenie x=2−3y (2−3y)²−6(2−3y)+y²−2y+2=0 4−12y+9y²−12+18y+y²−2y+2=0 10y²+4y−6=0 /2 5y²+2y−3=0 Δ=64 √Δ=8

	−2−8
y1=		=−1
	10

	−2+8		3
y2=		=
	10		5

x₁=2+3=5

	1
x2=
	5

	1		3
A=(5,−1) B=(		,		)
	5		5

	1		3
|AB|=√(		−5)2+(		+1)2
	5		5

	128
|AB|=√
	5

	8√10
|AB|=
	5

bezendu: poprawiam: Okrąg o równaniu x²−6x+y²−2y+2=0 i prosta x+3y+2=0 przecinają się w punktach A, B wyznacz długość cięciwy AB x=−2−3y (−2−3y)²−6(−2−3y)+y²−2y+2=0 4+12y+9y²+12+18y+y²−2y+2=0 10y²+28y+18=0 /2 5y²+14y+9=0 Δ=16 √Δ=4

	−14−4		9
y1=		=−
	10		5

	−14+4
y2=		=−1
	10

	37
x1=
	5

x₂=1

	37		9
A=(		,−		)
	5		5

B=(1,−1)

	4√65
AB=
	5

Bizon: ok

bezendu: Ale o którym mówisz ?

Bizon: ...chyba o żadnym −

bezendu: To już nie wiem gdzie źle liczę

Bizon: dla y=−9/5 x=−2+27/5=17/5

bezendu: OK dziękuję

Bizon: −

Eta:

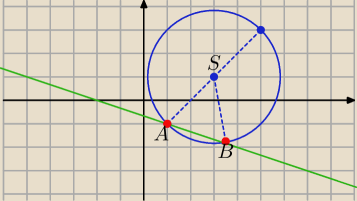
	17		9
A(1.−1) , B(		, −		)
	5		5

znajdź błąd w swoich rachunkach ......

Eta:

bezendu: Dziękuję, już wiem gdzie robiłem błąd

Bizon: ... Eta − Ty najwyraźniej "uganiasz się" za mną ... chyba na mnie lecisz −