Funkcje DeDee: Funkcja f określona jest wzorem f(x)=3^x2−3x²−1 Ile miejsc zerowych ma podana funkcja? Czy jest różnowartościowa? Czy jest parzysta?

DeDee: Kto podpowie jak to mogę rozwiązać?

Maniek: UP

Maniek: UP

Panko: D_f=R : ∀x∊R , −x∊R f(x)=f(−x) co widać gołym okiem . Jest parzysta ⇒ nie jest różnowartościowa. Co do miejsc zerowych , bez pochodnej. f(0)=0 f(1)=f(−1) <0 oraz ∀n>=2 3ⁿ>3n +1 stąd z własnoSci Darboux y=f(x) ma w przedziałach (−√2, −1 ), (1,√2) co najmniej po jednym jeszcze Nie wiem jak to doprecyzować

Maniek: Ktoś da radę pomóc z tymi miejscami zerowymi? Bo jestem w liceum, a pochodnych nie przerabialiśmy z naszą świetną nauczycielką

Maniek: UP, jeszcze raz proszę o jakieś wsparcie

Maniek: UP ta funkcja będzie miała więcej niż 3 rozwiązania?

Panko: Wrzuć to na Casio Graphics . I wtedy próbuj to uzasadnić . Jakie narzędzia są dozwolone ?

Maniek: Nie kojarzę takiego programu ani stronki, możesz linka zarzucić?

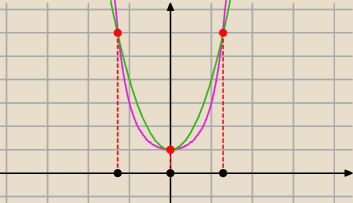
-:): ... jak widzisz ... ta funkcja ma 3 rozwiązania Rysunek obrazuje układ 3^x2=3x²+1

Panko: Mam na uwadze kalkulatory graficzne Casio. Narzędzia rachunkowe ? ( bez pochodnej ?)

MQ: Tu się często posługujemy stroną Wolfram Alpha

MQ: Macie: http://www.wolframalpha.com/input/?i=plot+3%5E%28x%5E2%29-3*x%5E2-1

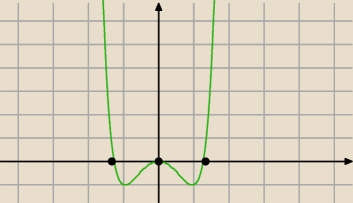
-:): ... więcej zaufania do tej stronki to jest wykres funkcji f(x)=3^x2−3x²−1

Maniek: wielka dziena! spoko stronka

Maniek: Niezbyt jeszcze ogarniam te stronke ale z czasem się do niej przyzwyczaje

-:): ... i nie narzekaj na nauczycielkę − Nie jest taka zła skoro "serwuje" Wam taką zabawę − Rozumiem, że to szkoła średnia ?

PW: 3^u = 3u+1, u > 0 ma dwa rozwiązania: x₁=0 i x₂ = 1. Myślę, że uczeń szkoły średniej w tym miejscu rysuje te dwa wykresy w jednym układzie współrzędnych i na tym kończy argumentację (nazywa to się uczenie "korzysta ze znajomości przebiegu tych funkcji"). Dowód elementarny 3^u > 3u + 1 dla x>1 jest możliwy, ale chyba się tego od ucznia nie wymaga.

-:): a niby skąd te x₂=1 ? −

Panko: A tak zapytam, jak po szkolnemu pokazać, że wykres f(u)=3^u , u∊R nie jest figurą osiowo symetryczną ? .

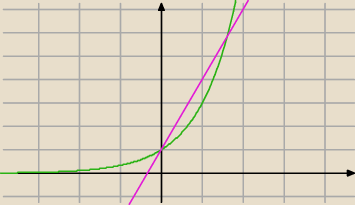
-:): ... i teraz "lustro" względem Oy jako, że podstawiliśmy n=x²

PW: Panko, takich pytań się nie zadaje w liceum. Uczeń zna tylko wzory na symetrię względem osi OX, OY i y=x.

-:): nie przesadzaj ... Odróżnić funkcję symetryczną względem Oy potrafi Rozkładając na dwie funkcje y=3^x2 i y=3x³+3 widzi, że obie są parzyste , nie są różnowartościowe Składając je itd ... zadanko dla ambitnych uczniów fajnej nauczycielki −

PW: − : ) : Opowiadasz jakieś czary. Co ma wynikać z tego "rozbijania" i "składania"? Funkcja jest parzysta f(x) = f(−x), nic więcej nie trzeba pokazywać. Parzystość to symetria wykresu względem osi OY. Ja odpowiadałem na pytanie Panko z 20:43

-:): ... czarów nie opowiadam Zauważ, że f(x)=3^x2−(3x²+1) ... nie widzisz składanki ?

Maniek: Zobaczyłem tu 3 wykresy, każdy miał coś podobnego, ale już nwm co jest dobrze niespecjalnie rozumiem całą składankę. Rozumiem, że moja nauczycielka jest fajna bo daje takie zadania, ale ona ich nie potrafi wytłumaczyć... zresztą czasami sama nie wie jak je zrobić. W tym jest problem, po co ktoś uczy czegoś czego nie umie nauczyć. Wtedy nic z tego nie mam. Tylko godziny przesiedziane nad zadaniem bez jakichkolwiek efektów. Na szczęście są takie stronki jak ta, gdzie ludzie pomogą, przeprowadzą dyskusję, coś wytłumaczą. Tak czy siak dziękuję wam wszystkim już teraz, bo na pewno nie raz się tutaj jeszcze odezwę

Maniek: Chciałbym jeszcze zapytać − czy w odpowiedzi powininno być, że równanie ma co najmniej czy miejsca zerowe, czy że ma dokładnie 3 miejsca zerowe? Jaka to różnica?