 X=<−π/2 , π/2> Y=<−1,1>
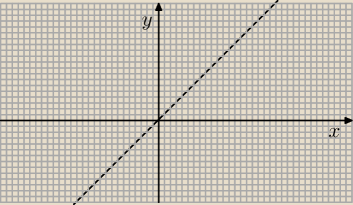
arcsin(sinx)= idx=x to tylko część definicji funkcji odwrotnej do y=f(x)=sinx
x∊X
czyli y=arcsin(sinx) = x , x∊X czyli wykresem jest odcinek prostej która jest
wykresem y=x
X=<−π/2 , π/2> Y=<−1,1>
arcsin(sinx)= idx=x to tylko część definicji funkcji odwrotnej do y=f(x)=sinx
x∊X
czyli y=arcsin(sinx) = x , x∊X czyli wykresem jest odcinek prostej która jest
wykresem y=x
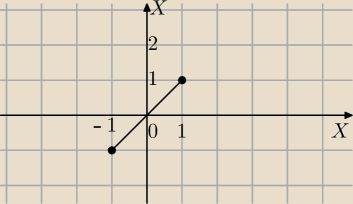 a)
f(x) =sin(arcsin(x)) , x∊<−1,1>
f(x)=x
a)
f(x) =sin(arcsin(x)) , x∊<−1,1>
f(x)=x
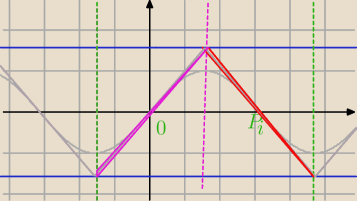 f(x)=arcsin(sin(x)), x∊R
f(x)=arcsin(sin(x)), x∊R
| −π | π | |||
Dla x∊< | , | > | ||
| 2 | 2 |
| π | 3π | −π | π | |||||
Dla x∊(U{ | , | > mamy: x=π+s, s∊( | , | > | ||||
| 2 | 2 | 2 | 2 |