Prawdopodobieństwo bezendu: ? Jeśli A⊂Ω i B⊂Ω To P(A∪B)=1 ? P(A∩B)=0 ?

Raferu: Jest taka możliwość lecz nie jest to zasada

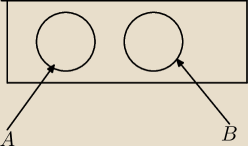
Raferu: Przykład że tak nie musi być

bezendu: No to może na zadaniu: Dane są zdarzenia A⊂Ω i B⊂Ω Takie, że A∪B=Ω Oblicz P(A−B) jeżeli wiadomo, że P(B')=0,3 P(B)=0,7 P(A)=1−0,7=0,3 P(A−B)=0,3−0=0,3

Piotr 10: ja to widzę tak P(A U B)=1 P(A − B)= P(A) − P(A ∩ B) P(A U B) = P(A) + P(B) − P(A∩ B) P(B)=0,7 P(A) − P(A∩ B)= P(A U B) − P(B)=1 − 0,7=0,3

bezendu: A jak to widzą inni ?

bezendu: A moje rozwiązanie jest ok ?

bezendu: ?

Mila: Nie możesz napisać ,że P(A)=1−P(B), tak byłoby dla zbiorów rozłącznych. Rozw. Piotra poprawne. P(AUB)=^dfP(A)+P(B)−P(A∩B)⇔ 1=P(A)+0,7−P(A∩B)⇔ 0,3=P(A)−P(A∩B)=^dfP(A\B) i koniec.

bezendu: Ale skoro A i B⊂Ω to ich suma musi wynosić 1 ?

bezendu: Tak czy nie ?

Mila: Nie.

bezendu: Ale wynik wyszedł ten sam ?

bezendu:

	1−P(A')
Wykaż, że jeśli P(B)>0 to P(A|B)≤
	P(B)

P(A)+P(B)−P(A∪B)		1−P(A')
	≤		/ P(B)
P(B)		P(B)

P(A)+P(B)−P(A∪B)≤1−P(A') P(A)+P(A')+P(B)−P(A∪B≤1 1+P(B)−1≤1 P(B)≤1 ok ?

bezendu: Jak zaznaczyć to na rysunku ?

bezendu: ?

bezendu: Da się wgl prawdopodobieństwo warunkowe zaznaczyć na tych diagramach ?

Mila: Zostaw warunkowe, nie będzie jutro.

bezendu: Ale w piątek może być ?

Hajtowy: Do piątku w kij czasu. Dasz radę

bezendu: Tak jak z dzisiejsza Lalką

Mila: Nie czytałeś?

bezendu: Czytałem ale w drugiej klasie, a teraz będąc w czwartej już zapomniałem. Po za tym nie spodziewałem się, że będzie Lalka.

Mila: Obejrzyj serial. Lalka przez ostatnie lata ciągle się gdzieś plącze, warto przeczytać. Tak samo "Przedwiośnie".

bezendu: Tylko w filmie Cezary jest zastrzelony a w książce nie

Eta:

jakubs: Ja również pisałem dzisiaj wypracowanie z Lalki. Do maja sporo czasu, według mnie wystarczy znać o co chodziło w poszczególnych lekturach i przynajmniej głównych bohaterów i to powinno wystarczyć na te minimalne 30%, a nawet więcej, no chyba że większe ambicje

bezendu: Eta

bezendu: Czy może ktoś sprawdzić to zadanie z 18:07 ?

bezendu: ?

bezendu: Dzięki za pomoc..

bezendu: Sprawdzi to ktoś kiedyś ? czy raczej nie ?

bezendu:

Trivial: Cześć bezendu.

bezendu: Cześć Sprawdzisz to zadanie ?

Trivial: Dlaczego nagle P(A∪B) = 1 pod końcem? Ja mam inny sposób.

	1 − P(A')
Tw. P(B) > 0 ⇒ P(A|B) ≤
	P(B)

P(A∩B)		1 − P(A')
	≤
P(B)		P(B)

P(A∩B) ≤ P(A) → OK.

bezendu: P(A)+P(A')=1 ?

Trivial: Tak.

bezendu: To dlatego mam 1

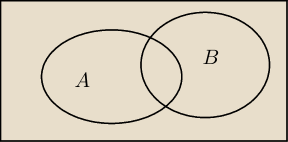
Trivial: No ale z tego nie można wywnioskować, że P(A∪B) = 1.

bezendu: Ok dzięki, mam jeszcze kilka takich zadań ? Masz czas ?

Trivial: Miałem robić projekt, ale chyba i tak się nie zbiorę. Dawaj.

bezendu: Dane są zdarzenia i A⊂Ω, B⊂Ω takie,że A∪B=Ω Oblicz P(A−B) jeżeli wiadomo, że P(B')=0,3 Wyznaczyłem P(B)=0,7 i P(A)=0,3 P(A∪B)=P(A)+P(B)−P(A\B) ?

Piotr 10: P(A − B)= P(A) − P(A∩B) P(B')=0,3 P(B)=0,7 P(A U B) =1 P(A)+ P(B) − P(A∩B) = 1 P(A) − P(A∩B) = 1 − P(B)=0,3 P(A − B)=0,3

bezendu: Czemu piszesz gotowe rozwiązanie ?

Piotr 10: Ok, sorry znikam