 Witam mam problem z tym zadaniem.
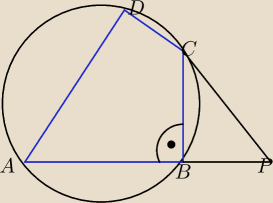
Na czworokącie ABCD opisano okrąg. Prosta DC przecina prostą AB w punkcie P, przy czym |AB| =
|BP| = 8cm. Wiedząc, że kąt ABC = 90 oraz |BC| = 6cm, oblicz pole czworokąta ABCD.
Z góry dziękuję za pomoc
Witam mam problem z tym zadaniem.
Na czworokącie ABCD opisano okrąg. Prosta DC przecina prostą AB w punkcie P, przy czym |AB| =
|BP| = 8cm. Wiedząc, że kąt ABC = 90 oraz |BC| = 6cm, oblicz pole czworokąta ABCD.
Z góry dziękuję za pomoc
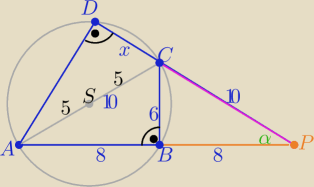 .............
i z tw. o siecznych : 8*16=10(x+10) ⇒ x=2,8
Pole czworokąta ABCD można obliczyć
np. tak :
sinα=3/5 , P(CBP)=24
.............
i z tw. o siecznych : 8*16=10(x+10) ⇒ x=2,8
Pole czworokąta ABCD można obliczyć
np. tak :
sinα=3/5 , P(CBP)=24
| 1 | 3 | |||
P(ABCD)=P(APD)−P(CBP)= | *16*12,8* | −24= ............ | ||
| 2 | 5 |
