 z.1
Funkcja f(x) = ( m2 − m − 6) x + 3 jest malejąca, gdy m2 − m − 6 < 0
Δ = (−1)2 − 4*1*(−6) = 1 + 24 = 25
√Δ = 5
z.1
Funkcja f(x) = ( m2 − m − 6) x + 3 jest malejąca, gdy m2 − m − 6 < 0
Δ = (−1)2 − 4*1*(−6) = 1 + 24 = 25
√Δ = 5
| 1 − 5 | 1 + 5 | |||
m1 = | = − 2 m2 = | = 3 | ||
| 2 | 2 |
 z.2
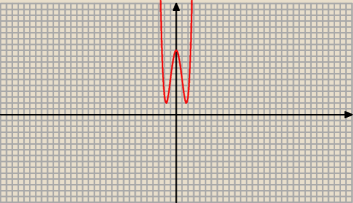
f(x) = x4 − 6 x2 + 11
f '(x) = 4 x3 − 12 x = 0 ⇔ 4x*( x2 − 3) = 0 ⇔ x = − √3 lub x = 0 lub x = √3
f " (x) = 12 x2 − 12
więc
f" ( −√3) = 12*3 − 12 = 24 > 0
f " (0) = − 12 < 0
f " ( √3) = 24 > 0
zatem funkcja f osiąga minimum lokalne dla x = − √3 i dla x = √3
Obliczamy:
f( − √3) = ( −√3)4 − 6*( − √3)2 + 11 = 9 − 6*3 + 11 = 2
oraz
f( √3) = ( √3)4 − 6*(√3)2 + 11 = 9 − 6*3 + 11 = 2
czyli funkcja f przyjmuje najmniejszą wartość równą 2.
ZWf = < 2; + ∞ )
=============
z.2
f(x) = x4 − 6 x2 + 11
f '(x) = 4 x3 − 12 x = 0 ⇔ 4x*( x2 − 3) = 0 ⇔ x = − √3 lub x = 0 lub x = √3
f " (x) = 12 x2 − 12
więc
f" ( −√3) = 12*3 − 12 = 24 > 0
f " (0) = − 12 < 0
f " ( √3) = 24 > 0
zatem funkcja f osiąga minimum lokalne dla x = − √3 i dla x = √3
Obliczamy:
f( − √3) = ( −√3)4 − 6*( − √3)2 + 11 = 9 − 6*3 + 11 = 2
oraz
f( √3) = ( √3)4 − 6*(√3)2 + 11 = 9 − 6*3 + 11 = 2
czyli funkcja f przyjmuje najmniejszą wartość równą 2.
ZWf = < 2; + ∞ )
=============