. Piotr 10: Z talii 52 kart losujemy 4. Oblicz prawdopodobieństwo, że wśród wylosowanych kart będą dwa króle lub dwie damy. Wynik podaj z dokładnością do 0,01.

	52 4
Ω=

	4 2		48 2		4 2		48 2
A=		*		+		*

	A
P(A)=
	Ω

Czy to jest dobrze? Zastanawiam się czy mogą jednocześnie wystąpić dwa króle i dwie damy

Eta: A czemu niby nie? 2 króle i 2 damy zawsze mogą być wśród 4 kart z tej talii 5 króli nie może być

Piotr 10:

	4 2		4 2
Czyli do zdarzenia A muszę jeszcze dodać A=.......+		*		, tak?

Piotr 10: Hmm ?

Piotr 10: Spośród siedmiu osób, wśród których jest Adam i Ewa wybieramy losowo trzy. Oblicz prawdopodobieństwo, że w wybranej trójce znajdzie się Adam i nie znajdzie się Ewa,

	7 3
Ω=

	6 3
A=

	A
P(A)=
	Ω

Dobrze myślę?

Piotr 10: Dane są P(A)=0,4 , P(B U A)=0,9 , P(B)=0,7. Oblicz P(B−A). P(B U A)=P(B) + P(A) − P(B ∩ A) P(B ∩ A)=0,2 P(B − A)=P(B) − P(B ∩ A) =0,7 − 0,2= 0,5 OK?

Eta: A : wybierasz 1 Adama i z pozostałych 5 osób ( bo bez Ewy i Adama) wybierasz 2 osoby

	1 1		5 2
|A|=		*

Piotr 10: Eta jak możesz to sprawdź mi zadania w tym poście. Z tymi kartami i z tym ostatnim

Eta: Zadanie z kartami: 2 króle lub 2 damy czyli A: 2 króle z 4 króli i 2 karty inne ( bez dam i króli) czyli z 46 kart 2 damy z 4 dam i 2 karty inne (bez dam i króli) z 46 2 damy i 1 król i 1 karta inna z 46 2 króle i 1 dama i 1 karta inna z 46

	4 2		46 2		4 2		4 1		46 1
|A|= 2*		*		+ 2*		*		*

Piotr 10: OK. Dziękuję Ja powrócę do tych zadań jutro. Dobranoc

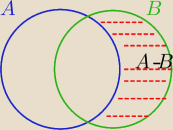
Eta: Zad z 23:53 ok Mogłeś też napisać,że P(A−B)= P(AUB)−P(A)= 0,9−0,4=0,5

Eta: Miłych snów

Piotr 10: A nie powinno być 44 zamiast 46?

daras: też tak myślę

daras: ≈0,04 ?