analityczna w przestrzeni, wyznaczenie prostej symetrycznej Kuczek: wyznacz prostą symetryczną do prostej bd względem prostej cd b (−2,4,6) c (−2 0 2) d (4 −6 −8)

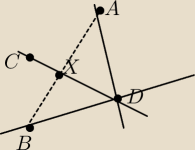
Kuczek: wyszło mi: x = −550/43t + 4 y = 206/43t − 6 z = 458−43t − 8 czy ktoś mógłby napisać mi czy dobrze rozumuję? Wyznaczyłem rzut punktu B na prostą CD (X). Następnie poprzez współrzędne środka odcinka wyliczyłem współrzędne punktu B odbitego symetrycznie względem prostej CD i otrzymałem punkt A. Wyliczyłem wektor AD i mam już wszystkie dane potrzebne do napisania równania prostej.

Kuczek: Proszę o pomoc

Kuczek: jeszcze raz odświeżam

AS: Moja propozycja Równanie prostej CD:

x − 4		y + 6		z+ 8
	=		=		lub w postaci parametrycznej
6		−6		−10

x = 4 + 6*t , y = −6 − 6*t , z = −8 − 10*t Wektor normalny; W = [6,−6,−10] Równanie płaszczyzny: 6*x − 6*y − 10*z + D = 0 Współrzędne punktu B wstawiam do równania płaszczyzny by znaleźć D 6*(−2) − 6*4 −10*6 + D = 0 => D = 96 Równanie płaszczyzny 6*x − 6*y − 10*z + 96 = 0 /:2 3*x − 3*y − 5*z + 48 = 0 Do ostatniego równania wstawiam x,y,z (z równania prostej),by znaleźć t 3*(4 + 6*t) − 3*(−6 − 6*t) − 5*(−8 − 10*t) + 48 = 0 => t = −59/43 Mając t wyliczam x,y,z z równania prostej x = −4 10/43, y = 2 10/43 , z = 5 31/43 , są to współrzędne rzutu punktu B na prostą CD. Jest on zarazem środkiem odcinka AB. Wystarczy znaleźć punkt A i napisać równanie AD