Prawdopodobieństwo-R bezendu: Ze zbioru liczb Z={−1,3,4,6,8,9} losujemy bez zwracania liczby x i y. Oblicz prawdopodobieństwo zdarzeń P(A), P(B) P(A∪B) jeśli A−suma wylosowanych liczb jest nieparzysta B−wylosowane liczby spełniają warunek 25<(x−1)²+y²≤100 Q=6*5=30 A−{(−1,4) (−1,6) (−1,8) (3,3) (3,6) (3,8) (4,−1) (4,3) (4,9) (6,−1) (6,3) (6,9) (8,−1) (8,3) (8,9) (9,4) (9,6) (9,8) } A=18

	18		3
P(A)=		=
	30		5

dalszy ciąg w nowym wątku

Piotr 10: w podpunkcie a) można bez wypisywania tych liczb wszystkich. Kiedy suma dwóch liczb da liczbę nieparzystą?

bezendu: Można nawet będzie tylko 12 możliwości ale poczekaj

Piotr 10: Wygląda ok te pierwsze zadanie. Ale to wiesz, ja to cieniznaaa z tego działu

bezendu: teraz do b tutaj rysunek http://static.pokazywarka.pl/i/2475035/280600.jpg B=24

	24		4
P(B)=		=
	30		5

	7		14		14
P(A∪B)=		−		=
	5		30		15

bezendu:

bezendu: Skusi się ktoś żeby to sprawdzić ?

bezendu: ?

bezendu:

bezendu: Czemu nikt nie chcę sprawdzić ?

Mila: a) |A|=2*3*3=18 {−1,3,9} ,{4,6,8} − losujesz nieparzystą i parzysta lub parzystą i nieparzystą. Dobrze obliczyłeś. b) za chwilę.

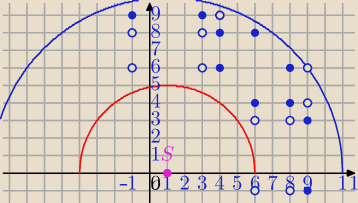
Mila: (−1,.) 3 punkty (3,..) 3 punkty (4,..) 3 punkty (6<..) 4 punkty (8,..) 4 punkty (9,..) 4 punkty |B|=21

	21		7
P(B)=		=
	30		10

|A∩B|=11

	6		7		11		13		11		39		11
P(AUB)=		+		−		=		−		=		−
	10		10		30		10		30		30		30

	28		14
P(AUB)=		=
	30		15

bezendu: Mila też robiłem tak jak Ty wypisując te punkty