przeksztalcenia zadanie: 1. Poslugujac sie dwoma rodzajami wzorow ogolnych dla izometrii plaszczyzny , wylicz wzory ich przeksztalcen odwrotnych i uzasadnij (na podstawie tych wzorow), ze sa one izometriami. Jakimi? Zrob to samo dla podobienstw. Odczytaj z uzyskanego wzoru jaka skale ma podobienstwo bedace przeksztalceniem odwrotnym do podobienstwa o skali k? izometrie: 1) x'=xcosα+ysinα+e y'=xsinα−ycosα+f xcosα+ysinα=x'−e xsinα−ycosα=y'−f z metody wyznacznikow wyliczam x: W=−cos²α−sin²α=−1 W_x=−x'cosα+ecosα−y'sinα+fsinα W_y=y'cosα−fcosα−x'sinα+esinα po zamienieniu oznaczen przeksztalcenie odwrotne: x'=xcosα+ysinα−ecosα−fsinα y'=xsinα−ycosα−esinα+fcosα jest ono izometria bo wyznacznik macierzy jest rowny −1. ale jaka? tego nie wiem 2 przypadek pomine

zadanie: podobienstwa: 1) x'=ax−by+e y'=bx+ay+f ; podobienstwo o skali k=Ie₁I=Ie₂I=I[a,b]I=I[−b,a]I ax−by=x'−e bx+ay=y'−f z metody wyznacznikow: W=a²+b² W_x=ax'−ae+by'−bf W_y=ay'−af−x'b+eb po zamienieniu oznaczen przeksztalcenie odwrotne:

	ax+by−ae−bf
x'=
	a2+b2

	−xb+ay+be−af
y'=
	a2+b2

jezeli to jest dobrze to jak uzasadnic, ze jest to podobienstwo?

	a		b
skala k1=I[		,		]I
	a2+b2		a2+b2

zadanie: 2. Czy przeksztalcenie x'=−2x+3y−4, y'=−3x−2y+2 jest a) izometria b) podobienstwem (jesli tak, to o jakiej skali)? Zbadaj, czy przeksztalcenie to ma punkt staly. a) wyznacznik macierzy m(T)=4+9=13 nie jest izometria bo wyznacznik macierzy nie jest rowny 1 ani −1. b) jest podobienstwem bo odpowiednie wspolczynniki sa zgodne ze wzorem ogolnym podobienstwa k=I[−2,−3]I=I√4+9I=I√13I=√13 punkt staly: T(P)=P P(x, y) x'=x⇔x=−2x+3y−4 y'=y⇔y=−3x−2y+2 z metody wyznacznikow: 3x−3y=−4 3x+3y=2 W=18; W_x=−6; W_y=18

	1
x=−
	3

y=1

	1
ma punkt staly P(−		, 1)
	3

zadanie: 3. Czy przeksztalcenia liniowe o nastepujacych macierzach sa izometriami? Odpowiedz uzasadnij. W przypadku negatywnej odpowiedzi wskaz wektor v, ktorego obraz ma dlugosc rozna od v. Wydaje mi sie, ze przeksztalcenia sa izometriami jezeli ich wyznacznik jest rowny 1 albo −1. det(M₁)=(1 0 0 0)=0−0=0; nie jest izometria; wyznacznik tej macierzy jest rowny 0, czyli to przeksztalcenie nie ma odwrotnego. to mozna wtedy podac przyklad? det(M₂)=(0 3/5

	3
1 −4/5)=−		; nie jest izometria
	5

np. jezeli nie jest to izometria to przyklady moga byc raczej dowolne. np. v=[4, 2] det(M₃)=(0 1 1 0)=0−1=−1; tak det(M₄)=(1 −1 1 1)=1+1=2; nie; np. v=[4, −5]

zadanie: prosilbym o sprawdzenie tych zadan i wytlumaczenie bledow?

Mila: Izometrie> zadanie 11:01 Obrót o kąt α wokół początku układu współrzędnych x'=xcosα−ysinα y'=xsinα+ycosα Nie wiem dlaczego zmieniłeś wzór. 1) Podobieństwa. Popatrz na zapisy na wykładzie ( było?) Przekształcenie F jest podobieństwem, jeżeli istnieje taka liczba s>0, że |F(A)F(B)|=s*|AB| 2) Podobieństwo jest różnowartościowe , a przekształcenie odwrotne do podobieństwa o skali s,

	1
jest podobieństwem o skali		.
	s

W zadaniu 1) 11:14

1		1
	=
s		√a2+b2

Uzasadniasz korzystając z udowodnionych tw. na wykładzie, albo z definicji wykazujesz. zadanie 2) 11:28, wystarczy podać konkretny przykład nie spełniający warunku izometrii i już jest obalone tw. punkt stały dobrze.

Mila: Zadanie 11:14

	ax+by−ae−bf
x'=
	a2+b2

	−xb+ay+be−af
y'=
	a2+b2

P(x₁,y₁) ,Q(x₂,y₂)− dwa dowolne punkty płaszczyzny |PQ|=√(x₂−x₁)²+(y₂−y₁)² P'(x'₁,y'₁) ,Q(x'₂,y'₂) punkty po przekształceniu punktów P i Q.

	ax1+by1−ae−bf		ax2+by2−ae−bf
x'1=		, x'2=
	a2+b2		a2+b2

	−x1b+ay1+be−af		−x2b+ay2+be−af
y'1=		, y'2=
	a2+b2		a2+b2

	ax2+by2−ae−bf		ax1+by1−ae−bf
|P'Q'|=[ (		−		)2+
	a2+b2		a2+b2

	−x2b+ay2+be−af		−x1b+ay1+be−af
+(		−		)2]12=
	a2+b2		a2+b2

	(a(x2−x1)+b(y2−y1))2+((x1−x2)b+(a(y2−y1)2)
=[		]12=
	(a2+b2)2

Piszę tylko licznik: ={a²(x₂−x₁)²+2a*b(x₂−x₁)(y₂−y₁)+b²*(y₂−y₁)²+b²(x₁−y₂)²+ −2a*b(x₂−x₁)(y₂−y₁)+a²((y₂−y₁)²= wracam do ułamka

	(x2−x1)2(a2+b2)+(y2−y1)2(a2+b2)
=[		]12=
	(a2+b2)2

	√(x2−x1)2+(y2−y1)2		1
=		=		*|PQ|
	√a2+b2		√a2+b2

Przekształcenie jest podobieństwem o skali

	1
k=
	√a2+b2

zadanie: dziekuje a zadanie 2 skala jest dobrze obliczona? i to uzasadnienie, ze jest to podobienstwo? jako tako my nie udowadnialismy nic o izometriach i podobienstwach a we wczesniejszych przeksztalceniach powolywalismy sie na wzor, czyli tutaj: jest to podobienstwo bo odpowiednie wspolczynniki przy zmiennych sa zgodne ze wzorem. odnosnie zadania 1 to nie rozumiem o co chodzi z ta zmiana wzoru? mielismy podane 2 przypadki wzorow dla izometrii. Jeden z nich napisalem a drugi pominalem. Tylko tam bylo jeszcze pytanie Jakimi? sa po tym przeksztalceniu odwrotnym i tego wlasnie nie wiem. a zadanie 3 jest poprawne? bo tak chyba najszybciej mozna sprawdzic czy jest to izometria?

Mila: 21:50, pokazałam ten żmudny sposób wykazywania, że jest to podobieństwo i od razu obliczyłam skalę. w zadaniu 1. Można pokazać, że dane przekształcenie jest podobieństwem, w takim razie odwrotne

	1
też i skala odwrotnego to
	s

Jeśli korzystacie z wzorów, to dobrze. To najszybciej. Na pewno masz dowody na wykładzie. Zadanie 3 dobrze, M3 −izometria x'=y y'=x a to jest symetria względem prostej y=x Mogę Ci napisać kilka podstawowych przekształcen z nazwami. Gdzieś to mam zapisane, jak znajdę i przydadzą się, to napiszę.Jeśli masz , to nie będę pisała.

zadanie: to znaczy przeksztalcenia liniowe, afiniczne, izometrie i podobienstwa to mam.

Mila: 1) x'=xcosα−ysinα y'=xsinα+ycosα izometria −obrót o kąt α wokół P(0,0) 2) x'=xcosα+ysinα y'=xsinα−ycosα izometria− obrót o kąt α wokół P(0,0), i S_OX S_OX x'=x y'=−y Określ przekształcenie M1.

zadanie: wroce do tego w srode

zadanie: M1: x'=x y'=0 jest to rzut prostokatny

Mila: Na oś X.

zadanie: znajdz (za pomoca wzorow) wszystkie podobienstwa o skali 2, ktore zmieniaja orientacje plaszczyzny,i ktore przeksztalcaja os Ox na prosta x=2. k=2; k=√a²+b² podobienstwo, ktore zmienia orientacje plaszczyzny ma wzor: x'=ax+by+e y'=bx−ay+f os Ox czyli prosta y=0 jest przeksztalcana na prosta x=2 dalej jakies wskazowki?

zadanie: ?

zadanie: zrobilismy tak: a²+b²=4 x'=0x+2y+2 y'=2x−0y+f x'=0x−2y+2 y'=−2x−0y+f dlaczego a=0?

Mila: A wiesz dlaczego e=2?

zadanie: bo punkt (0,0) na osi 0x przechodzi na prosta x=2 czyli wstawiajac za x i y przy x' 0 zostaje e=2 a y' f jest dowolne chyba dobrze rozumiem? a co z a?

Mila: k=2 i k=√a²+b²⇔a²+b²=4 x'=2 dla punktów (x,0), x∊R Obraz punktu(0,0) x'=a*0+b*0+e=2⇔e=2 y'=b*0−a*0+f, y'∊R Obraz punktu (1,0) x'=a*1+b*0+2=2⇔a*1=0⇔a=0 a²+b²=4 b²=4⇔b=2 lub b=−2 1)x'=0x+2y+2 y'=2x−0*x+f 2) x'=0x−2y+2 y'=−2x+0y+f

zadanie: a dlaczego obraz punktu (1,0)?

Mila: Możesz wybrać inny punkt osi X, gdy masz ustalone e=2. (2,0) x'=a*2+b*0+2=2⇔a*2=0⇔a=0

zadanie: dziekuje

Mila:

zadanie: Znajdz wszystkie przeksztalcenia afiniczne T, ktore jednoczesnie spelniaja wszystkie warunki −przeprowadzaja os ox na prosta x=4 −sa podobienstwem nie zmieniajacym orientacji o skali 2 −punkt (0,0) jest odlegly o 5 od swojego obrazu T: x'=ax+by+e y'=bx+ay+f 1 warunek: punkt (0,0)→(4,?) 2. wzor podobienstwa wyzej, skala k=2 3 warunek: (0,0)→P; d((0,0), P)=5 podpowiedzi?

zadanie: ?

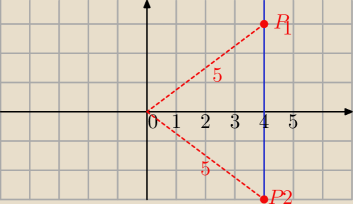
Mila: P₁=(4,3) P₂=(4,−3) |OP₁|=|OP₂|=5

zadanie: x'=0x−2y+4 y'=2x+0y±3 x'=0x+2y+4 y'=−2x+0y±3 czyli sa 4 takie przeksztalcenia

zadanie: chyba dobrze?

Mila: Czy zachowany warunek , że nie zmienia się orientacja ( Chyba W>0?)

zadanie: orientacja ma sie nie zmieniac czyli W>0 0*0−(−2)*2=4>0 0*0−2*(−2)=4>0

Mila: ?) Zobacz prawd., bo zaraz odchodzę od komputera.