równanie kwadratowe z wartością bezwzględną i parametrem Wiesiu: mam narysować wykres funkcji g(k), która każdej wartości parametru k przyporządkowuje liczbę rozwiązań równania |x²+2x−3|=k|x+3| ale nie wiem jak rozwiązać to równanie. Proszę o pomoc.

MQ: Zauważ, że x²+2x−3=(x−1)(x+3)

Eta:

	(x−1)(x+3)
I		|=k , x≠ −3
	x+3

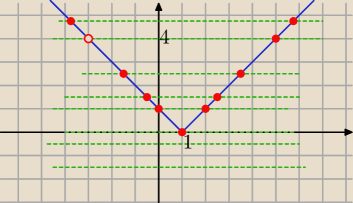
|x−1|=k i x≠ −3 0 rozwiązań dla k<0 1 rozwiązanie dla k=0 i k= 4 2 rozwiązania dla k ∊(0,4) U (4,∞)

Eta:

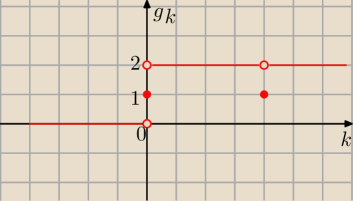
pigor: ..., narysować wykres funkcji g(k), która każdej wartości parametru k przyporządkowuje liczbę rozwiązań równania |x²+2x−3|= k |x+3| . −−−−−−−−−−−−−−−−−−− |x²+2x−3|= k |x+3| ⇔ |x+3] |x−1|−k |x+3|= 0 ⇔ |x+3| (|x−1|−k)= 0 ⇔ ⇔ x+3= 0 lub |x−1|= k ⇔ x= −3 lub |x−1|= k , więc { 1 dla k< 0 g(k)={ − szukana funkcja g zmiennej k . ... { 2 dla k ≥ 0

matyk: Niestety, ale oboje macie źle To równanie ma czasem nawet 3 rozwiązania

pigor: hmm ..., no to pochwal się np. przykładem, że masz rację . ...