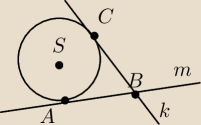
Geometria analityczna - okrąg styczny do prostej. jakubs: Mam takie zadanko: Znajdź równanie okręgu, który jest styczny do prostej k: x+y+13=0, natomiast do proste m: 7x−y−5=0 jest styczny w punkcie A(1,2). Mam pytanie, czy mogę wykorzystać twierdzenie o odcinkach stycznych tzn. |AB|=|BC| ? Oraz, że |SA|=|SC|. Punkt przecięcia się prostych to B(−1,−12)

jakubs: Zadanie rozwiązane, nie dałem rady wyznaczyć punktu C, ale wyznaczyłem sobie prostą przechodzącą przez S i A prostopadłą do prostej m.

+_: Oblicz współ.B=(−1,−12) następnie długość odcinka BC=√200,zakreślasz okrąg o promieniu R=BC który przecina prostą m w A=(−11,−2) o współrzędnych wylicz, następnie wyznaczasz proste prostopadłe do m i k w punktach A i C, przecięcie tych prostych to S=(−6,3), promień r=√50 to formalność