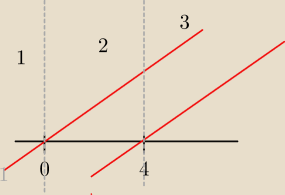
rozwiąż równanie Warum: IxI− 2Ix−4I =8−x 1) x∊(−∞,0) 2) x∊<0,4) 3) x∊<4,∞) i teraz nie wiem, kiedy w powyższych rozpiskach nawiasy powinny być otwarte bądź zamknięte (poza ∞ − wtedy zawsze otwarty) taki sam problem mam jeszcze w przypadku obu funkcji malejących, oraz gdy jedna jest malejąca, druga rosnąca

Warum: pomoże ktoś?

Bizon: ... napisałeś dobrze Dalej: 1^o −x−2[−(x−4)]=8−x −x+2x−8=8−x ⇒ 2x=16 ⇒ x=8 czyli nie ma rozwiązań w tym przedziale ...itd

5-latek: To jest obojetne jak zapiszez czy tak jak zapisales teraz czy tak x∊(−∞0> x∊(0,4> i x∊(4,∞) Teraz rozwiazujesz to rownanie w tych 3 przedzialach , Powiedz co oznaczaja te czewone kreski

Warum: to ma być dla ułatwienia w jakim przedziale funkcja (znaczy ten moduł) maleje, a kiedy rośnie

5-latek: Dobrze Licz dalej to rownanie tutaj

bezendu: IxI− 2Ix−4I =8−x 1⁰ (−∞,0) −x−2(−x+4)=8−x −x+2x−8=8−x x−8=8−x 2x=16 x=8∉(−∞,0) 2⁰ <0,4) x−2(−x+4)=8−x x+2x−8=8−x 3x−8=8−x 4x=16 x=4∉<0,4) 3⁰ <4,∞) x−2(x−4)=8−x x−2x+8=8−x −x+8=8−x x∊<4,∞)

Hajtowy: bezendu ... 5−latek Ci tego nie daruje Będzie zły

bezendu:

Warum: ogólnie te równania mi wychodzą, tylko była sytuacja pod tablicą, że matematyk przyczepił się do kolejności nawiasów ale nie chciał uzasadnić (nie zabijajcie bezendu)