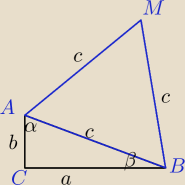
Punkty A, B, C są wierzchołkami trójkąta prostokątnego o przeciwprostokątnej AB, kamczatka: Punkty A, B, C są wierzchołkami trójkąta prostokątnego o przeciwprostokątnej AB, a punkty A, B, M wierzchołkami trójkąta równobocznego. Oblicz iloczyn sinusów kątów ostrych trójkąta ABC wiedząc, że pole tego trójkąta jest pięć razy mniejsze niż pole trójkąta ABM. Rozwiązanie: a,b−przyprostokątne c−przeciwprostokątna

a		b		ab
	*		=
c		c		c2

	1		c2√3		1		c2√3
5*		ab=		i skąd wiadomo że 5*		ab =		?
	2		4		2		4

sushi_ gg6397228: przeczytaj ostatnie zdanie od , że...

Bizon: ... z treści zadania wiadomo.

	ab
Ty masz przekształcać tak to wyrażenie aby policzyć z niego
	c2

kamczatka: nie ma podanego pola trójkąta ABM i właśnie nie wiem skąd to się wzięło.

Bizon: czytaj , aż zrozumiesz treść zadania−

Eta:

	a*b		c2√3
5*		=
	2		4

10ab= √3*c²

ab

√3

a

b

√3

√3

=

⇒

*

=

⇒ sinα*sinβ=

c2

10

c

c

10

10

dero2005: c² = a² + b²

a*b		c2√3		(a2+b2)√3
	*5 =		⇒ a*b =
2		4		10

	a
sinα =
	c

	b
sinβ =
	c

	a*b		(a2+b2)√3   10		√3
sinα*sinβ =		=		=
	c2		a2+b2		10

kamczatka: pole tego większego trójkąta z jakiego wzoru zostało obliczone ?

dero2005: wzór na pole trójkąta równobocznego przedstawia się jak niżej

	a2√3
P =		gdzie: a − bok trójkąta
	4

kamczatka: dobra juz mam