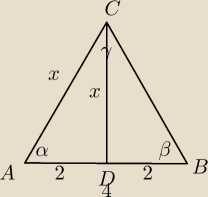
 Środkowa CD trójkąta ABC jest równa bokowi AC. Wyznacz kąty trójkąta ABC wiedząc, że |AB|=4 i
|BC|=2√3.
z Pitagorasa wyliczyłem x=√2
i później miałem pomysł aby z sinα obliczyć kąt i wyszedł 90 stopni
potem z tgβ=45 stopni
γ=180−(45+90)=45
ale w odpowiedziach mam inne wyniki powinno wyjść 30,60,90 stopni
Środkowa CD trójkąta ABC jest równa bokowi AC. Wyznacz kąty trójkąta ABC wiedząc, że |AB|=4 i
|BC|=2√3.
z Pitagorasa wyliczyłem x=√2
i później miałem pomysł aby z sinα obliczyć kąt i wyszedł 90 stopni
potem z tgβ=45 stopni
γ=180−(45+90)=45
ale w odpowiedziach mam inne wyniki powinno wyjść 30,60,90 stopni
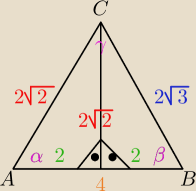

 Źle narysowaliśmy tamto, gdyż skoro długości |AC| i |CD| są takie same, to nie może być |CD|
wysokością trójkąta, gdyż to jest nielogiczne nawet
Źle narysowaliśmy tamto, gdyż skoro długości |AC| i |CD| są takie same, to nie może być |CD|
wysokością trójkąta, gdyż to jest nielogiczne nawet 
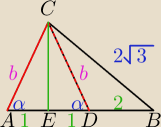
| BE | 3 | √3 | ||||
cos ∡B = | = | = | ⇒ ∡B = 30o | |||
| BC | 2√3 | 2 |
| CE | 1 | ||
= sin∡B = | ⇒ CE = √3 | ||
| BC | 2 |
| CE | ||
tg ∡ A = | = √3 ⇒ ∡A = 60o | |
| AE |
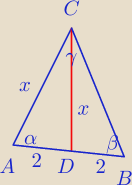 I AB I = 4
I BC I = 2√3
I AD I = I BD I = 2
Z tw. kosinusów mamy
x2 = 42 + (2√3)2 − 2*4*2√3 cos β = 16 + 12 − 16√3 cos β = 28 − 16√3 cos β
oraz
x2 = 22 + ( 2√3)2 − 2*2*2√3 cos β = 4 + 12 − 8 √3 cos β = 16 − 8√3 cos β
więc
28 − 16 √3 cos β = 16 − 8 √3 cos β
8 √3 cos β = 12
I AB I = 4
I BC I = 2√3
I AD I = I BD I = 2
Z tw. kosinusów mamy
x2 = 42 + (2√3)2 − 2*4*2√3 cos β = 16 + 12 − 16√3 cos β = 28 − 16√3 cos β
oraz
x2 = 22 + ( 2√3)2 − 2*2*2√3 cos β = 4 + 12 − 8 √3 cos β = 16 − 8√3 cos β
więc
28 − 16 √3 cos β = 16 − 8 √3 cos β
8 √3 cos β = 12
| 12 | 3 | √3 | ||||
cos β = | = | = | ⇒ β = 30o | |||
| 8√3 | 2√3 | 2 |
| √3 | ||
x2 = 16 − 8 p{3]*cos 30o = 16 − 8*√3* | = 16 − 12 = 4 | |
| 2 |
 I AB I = 4
I BC I = 2√3
I AD I = I BD I = 2
Z tw. kosinusów mamy
x2 = 42 + (2√3)2 − 2*4*2√3 cos β = 16 + 12 − 16√3 cos β = 28 − 16√3 cos β
oraz
x2 = 22 + ( 2√3)2 − 2*2*2√3 cos β = 4 + 12 − 8 √3 cos β = 16 − 8√3 cos β
więc
28 − 16 √3 cos β = 16 − 8 √3 cos β
8 √3 cos β = 12
I AB I = 4
I BC I = 2√3
I AD I = I BD I = 2
Z tw. kosinusów mamy
x2 = 42 + (2√3)2 − 2*4*2√3 cos β = 16 + 12 − 16√3 cos β = 28 − 16√3 cos β
oraz
x2 = 22 + ( 2√3)2 − 2*2*2√3 cos β = 4 + 12 − 8 √3 cos β = 16 − 8√3 cos β
więc
28 − 16 √3 cos β = 16 − 8 √3 cos β
8 √3 cos β = 12
| 12 | 3 | √3 | ||||
cos β = | = | = | ⇒ β = 30o | |||
| 8√3 | 2√3 | 2 |
| √3 | ||
x2 = 16 − 8 p{3]*cos 30o = 16 − 8*√3* | = 16 − 12 = 4 | |
| 2 |
 I AB I = 4
I BC I = 2√3
I AD I = I BD I = 2
Z tw. kosinusów mamy
x2 = 42 + (2√3)2 − 2*4*2√3 cos β = 16 + 12 − 16√3 cos β = 28 − 16√3 cos β
oraz
x2 = 22 + ( 2√3)2 − 2*2*2√3 cos β = 4 + 12 − 8 √3 cos β = 16 − 8√3 cos β
więc
28 − 16 √3 cos β = 16 − 8 √3 cos β
8 √3 cos β = 12
I AB I = 4
I BC I = 2√3
I AD I = I BD I = 2
Z tw. kosinusów mamy
x2 = 42 + (2√3)2 − 2*4*2√3 cos β = 16 + 12 − 16√3 cos β = 28 − 16√3 cos β
oraz
x2 = 22 + ( 2√3)2 − 2*2*2√3 cos β = 4 + 12 − 8 √3 cos β = 16 − 8√3 cos β
więc
28 − 16 √3 cos β = 16 − 8 √3 cos β
8 √3 cos β = 12
| 12 | 3 | √3 | ||||
cos β = | = | = | ⇒ β = 30o | |||
| 8√3 | 2√3 | 2 |
| √3 | ||
x2 = 16 − 8 p{3]*cos 30o = 16 − 8*√3* | = 16 − 12 = 4 | |
| 2 |