Miejsca zerowe? [N[ELO]]: Miejsca zerowe dwóch funkcji liniowych są liczbami odwrotnymi. Wykresy tych funkcji przecinają się w punkcie (0;3) i wraz z osią OX ograniczają trójkąt o polu 4. Wyznacz wzory tych funkcji. Zacząłem robić tak: pierwsza liczba to a a druga to ¹_a czyli ¹₂*(a−¹_a)*3=4 i co dalej? liczyłem tak: 3a²−8a−3=0 Δ=100 √Δ=10 x₁=−¹₃ x₂=3 i co dalej? skąd mam wiedzieć które x wziąć? to nie są liczby odwrotne bo są też przeciwne

[N[ELO]]:

ICSP:

	1
a co to jest a −
	a

[N[ELO]]: długość a ze wzoru ¹₂*a*h na pole trójkąta

ICSP:

	1
a −		na pewno nie jest długością.
	a

	1
Np dla a =		:
	2

1		3
	− 2 = −		< 0
2		2

a długość jak wiesz nie może być ujemna.

[N[ELO]]: to jak to oznaczyć?

ICSP:

	1
|a −		| − to będzie odległość. Oczywiście dla a ≠ 0
	a

[N[ELO]]: no to jak to policzyć dalej?

[N[ELO]]: mogółbym prosić o oblicznia?

ICSP: masz proste równanie :

	1		8
|a −		| =
	a		3

[N[ELO]]: i tu trzeba 2 przypadki rozważyć?

[N[ELO]]: i co dalej? jeżeli |a−¹_a|>=0 to mamy x₁=−¹₃ i x₂=3 a jak |a−¹_a|<0 to mamy x₁=¹₃ i x₂=−3

ICSP:

	1		1
Jeżeli a −		≥ 0 i to samo do drugiej: a −		< 0
	a		a

Sprawdzamy dla tego co znajduje się pod wartością bezwzględną a nie dla samej wartości bezwzględnej. czyli z pierwszego x = 3

	1
oraz z drugiego x =
	3

Zatem

	1
1o x = 3 oraz x =
	3

	1
2o x = −3 oraz x = −
	3

Teraz napisanie wzorów tych 4 funkcji liniowych nie powinno być problemem(po 2 funkcje dla każdego przypadku)

[N[ELO]]: 1^o to jest 1 funkcja a 2^o to jest druga funkcja. jak 4 przypadki?

[N[ELO]]: jak 4 funkcje*

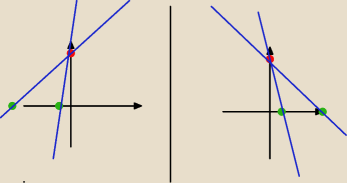
ICSP: 4 funkcje Po dwie dla każdego przypadku 1^o − pierwszy przypadek (rysunek z lewej ) 2^o − drugi przypadek (rysunek z prawej)

ICSP: Na odwrót : /

	1
Po lewej jest drugi przypadek tzn gdy x = −		oraz x = −3
	3

	1
Po prawej jest pierwszy przypadek gdy x =		oraz x = 3
	3