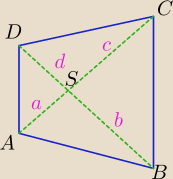
. Piotr 10: Dany jest czworokąt ABCD .Niech S będzie punktem przecięcia jego przekątnych. Udowodnij, że

	|AS|		IBSI
czworokąt ABCD można wpisać w okrąg wtedy i tylko wtedy, gdy		=		.
	IDS|		ICS|

Dowód trzeba przeprowadzić w dwie strony w formie implikacji (==>) I∡ASBI=I∡DSC) − kąty wierzchołkowe I∡SBAI=I∡DCSI − kąty wpisane oparte na tym samym łuku Jeżeli dwa trójkąty mają dwa kąty równe, to miara trzeciego kąta jednego i drugiego trójkąta muszą być sobie równe. Na podstawie cechy kkk ΔASB ∼ ΔDCS.

	IASI		IBSI
A więc		=
	IDSI		ICSI

(<==) I∡ASBI=I∡DSC) − kąty wierzchołkowe

	IASI		IBSI
		=
	IDSI		ICSI

Na podstawie cechy bkb ΔASB ∼ ΔDCS. A więc I∡SBAI=I∡DCSI ΔDAS ∼ ΔCSB (ceca bkb) I∡SCBI=I∡ADSI Zatem I∡BADI=180⁰ − I∡DCBI I∡CBAI=180⁰ − I∡ADCI Proszę o sprawdzenie, bo nie jestem pewny