prostopadłościan
ktosia: suma krawędzi prostopadłościanu o podstawie kwadratowe jest równa 16 wyznacz długości krawędzi
tak aby pole powierzchni całkowitej tego prostopadłościanu było największe,
W jaki sposób uwzględnić to że pole ma być największe


21 lis 22:21
ktosia: może jednak?
21 lis 23:29
Janek191:
x − długość krawędzi podstawy
y − długość krawędzi bocznej
Mamy
8x + 4y = 16 / : 4
2x + y = 4 ⇒ y = 4 − 2x
P
c = 2 x
2 + 4 x*y = 2x
2 + 4x*(4 − 2x) = 2 x
2 + 16x − 8x
2 = − 6x
2 + 16 x
więc
P
c(x) = − 6 x
2 + 16 x
a = − 6 < 0 , więc funkcja P
c (x) posiada największą wartość dla
| | 4 | | 12 | | 8 | | 4 | |
Wtedy y = 4 − 2* |
| = |
| − |
| = |
| |
| | 3 | | 3 | | 3 | | 3 | |
| | 4 | |
Mamy x = y. Tym prostopadłościanem jest sześcian o krawędziach długości x = |
| . |
| | 3 | |
21 lis 23:30
ktosia: dzięki

21 lis 23:37
Janek191:
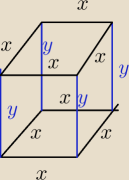
21 lis 23:41
ktosia: mam jeszcze takie zadanie: obliczyć dla jakich wartości parametru a, b liczba −2 jest
pierwiastkiem wielomianu w(x)=x
3+6x
2+ax+b, a reszta z dzielenia tego wielomianu prze (x−3)
jest równa 5. wykaż, że pozostałe dwa pierwiastki wielomianu są niewymierne.
Wartość a i b policzyłam −−−−> a=(−12) b=(−40)
Podstawiłam te wartości do wielomianu, ale nie mam pojęcia jak udowodnić że pozostałe dwa
pierwiastki są niewymierne

21 lis 23:42
ktosia: 
21 lis 23:54
Janek191:
W(x) = x
3 + 6 x
2 + ax + b
W(−2) = 0 ⇔ (−2)
3 + 6*(−2)
2 − 2 a + b = 0 ⇔ − 8 + 24 − 2a + b = 0 ⇔
⇔ 16 − 2a + b = 0
W(3) = 5 ⇔ 3
3 + 6*3
2 +3a + b = 5 ⇔ 27 + 54 + 3a + b = 5 ⇔
⇔ 81 + 3a + b = 5
Mamy układ
− 2a + b = − 16
3a + b = − 76
−−−−−−−−−−−−−−−−−− odejmujemy stronami
5a = − 60
a = − 12
======
b = − 16 + 2a = − 16 − 24 = − 40
===========================
więc
W(x) = x
3 + 6 x
2 − 12 x − 40
− 2 jest pierwiastkiem, więc W(x) dzieli się przez x + 2
czyli mamy
( x
3 + 6 x
2 − 12 x − 40 ) : ( x + 2) = x
2 + 4x − 20
−x
3 − 2 x
2
−−−−−−−−−−−−
4 x
2 − 12 x
− 4 x
2 − 8 x
−−−−−−−−−−−−−
− 20 x − 40
20 x + 40
−−−−−−−−−−
0
x
2 + 4x − 20 = 0
Δ = 16 − 4*1*(−20) = 16 + 80 = 96 = 16*6
√Δ = 4
√6
| | − 4 − 4√6 | |
x = |
| = − 2 − 2√6 |
| | 2 | |
lub
| | − 4 + 4√6 | |
x = |
| = − 2 + 2√6 |
| | 2 | |
22 lis 00:42





