funkcja Radek: Funkcja f określona jest wzorem f(x)=(3m −5)x²−(2m−1)x+0,25(3m−5) . Wyznacz te wartości parametru m∈ R, dla których najmniejsza wartość funkcji f jest liczbą dodatnią. 3m−5>0 3m>5

	5
m>
	3

Δ<0 (−2m+1)²−4(3m−5)(0.75m−1,25) 4m²−4m+1−4(2,25m²−3,75m−3,75m+6,25) 4m²−4m+1−4(2,25m²−7,5+6,25) 4m²−4m+1−9m²+30m−25 −5m²+26m−24<0 Δ_m=26²−4*(−5)*)−24) Δ_m=196 √Δ_m=14

	−26−14
m1=		=4
	−10

	−26+14		6
m2=		=
	−10		5

	6
m∊(−∞,		)∪(4,∞)
	5

ostatecznie m∊(4,∞) Proszę o sprawdzenie zapisu i obliczeń

Alfa: jest ok

Radek: Dzięki a takie coś Napisz wzór i narysuj wykres funkcji y = g(m ), która każdej liczbie rzeczywistej m przyporządkowuje najmniejszą wartość funkcji kwadratowej f (x) =−x² + (m²−4)x+ 2 w przedziale <− 1,1> .

Radek: ?

Radek: Jest tu ktoś wgl na tym forum ?

Hajtowy: Tak

Hajtowy: f(−1) oraz f(1) policz

Radek: To może ktoś mi wytłumaczyć to zadnie≠podanie rozwiązania,przepisanie rozwiązania z internetu ?

Hajtowy: Następnie f(−1) < f(1) Później masz rozwiązanie.... {f(−1) = coś dla m ∊ ... [Tu będzie rozwiązanie f(−1) < f(1) ] {f(1) = coś dla m ∊ ...

Hajtowy: Dziś Piotr 10 pomagałem z tym zadaniem.

Radek: f(−1)=−(−1)²+(m²−4)*(−1)+2 f(−1)=−1−m²+4+2 f(−1)=−m²+4+5 f(1)=−1+m²−4+2 f(1)=m²−3

Hajtowy: f(−1) źle

Hajtowy: f(−1)=−1−m²+4+2 ≠ f(−1)=−m²+4+5

Radek: −1−m²+4+2 −m²+5

Hajtowy: Git. Teraz f(−1) < f(1) Rozwiąż tą nierówność

Radek: A czemu należy rozwiązać taką nierówność ?

Hajtowy: Najpierw liczysz wartości w końcach przedziału <−1;1> czyli f(1) i f(−1) To teraz musisz sprawdzić, kiedy druga z tych liczb jest większa od pierwszej. Inaczej mówiąc: kiedy dla x=1 będzie wartość mniejsza tejże funkcji : −m² + 5 < m² + 3

ZKS: Takie pytanko a dlaczego nie rozpatrujemy x_w? Pytam czy rozumiesz zadanie do końca.

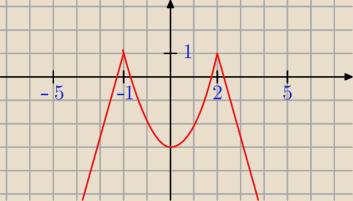
Hajtowy: {f(−1) = −m²+5 dla m ∊ (−oo;−2) ∪ (2;+oo) {f(1) = m²−3 dla m ∊ [−2;2] I to jest Twoje funkcja g(m)

Radek: O cześć ZKS liczyłem, że wejdziesz ! nie policzę f(x_w)

ZKS: Policzysz. Tylko dlaczego nie rozpatrujemy x_w. Może Hajtowy Ci pomoże i odpowie.

Radek: Ja bym wolał żebyś Ty mi wytłumaczył nie mam nic do Hajtowego ale jak ostatnio mi wytłumaczyłeś to wszystko rozumiałem

ZKS: Okej to od początku. Czego nie rozumiesz?

Radek: A jeszcze ta funkcja nie będzie miała największej wartości bo a<0 dlatego nie liczę wierzchołka ?

ZKS: Tak o to chodzi dla x_w mamy wartość największą bo a < 0. My poszukujemy najmniejszych wartości więc możemy olać x_w.

Radek: Czyli teraz mam policzoną wartość na końcach przedziałów i co dalej ?

ZKS: Jak policzysz to musisz porównać te wartości dla jakich m f(−1) jest mniejsze od f(1) ponieważ szukamy wartości najmniejszych. Rozumiesz? Jeżeli nie to pisz.

Radek: No tak ale nie wiem czy f(−1) czy f(1) będzie najmniejszą wartością ?

ZKS: Dlatego liczymy dla jakich m wartość funkcji dla x = 1 będzie większe od wartości funkcji dla x = −1. Należy zatem policzyć dla jakich m f(−1) < f(1) i dla tych m naszą najmniejszą wartością będzie f(−1).

Radek: Ale czemu f(−1)<f(1) a nie na odwrót ?

Lemon: Czyli rownie dobrze mozesz dać warunek f(1)<f(−1) i wtedy najmniejsza wartosc będzie dla x=1

Radek: Lemon to właśnie napisałem

ZKS: Nie ma różnicy jak policzysz jeżeli przyjmiesz f(−1) > f(1) to z tego otrzymasz dla jakich m wartości funkcji f(1) będą mniejsze od wartości f(−1). Zobacz sam.

Radek: Dobra jutro wstawię rozwiązanie Dziękuję jak będziesz jutro to rzuć okiem, bo coraz mnie osób na tym forum pomaga

ZKS: To napiszę na sam koniec. Szukasz wartości najmniejszych więc jeżeli policzysz dla jakich m f(−1) < f(1) to dla tych m wartością najmniejszą będzie funkcja g(m) = f(−1) = −m² + 5. Natomiast dla pozostałych m wartością najmniejszą będzie funkcja g(m) = f(1) = m² + 3. Mam nadzieję że to zrozumiesz. Złe odczułeś wrażenie nie mniej osób pomaga tylko te osoby które pomagają również pracują bądź studiują i nie raz nie mają czasu nawet zajrzeć na forum. Nie ma za co i powodzenia w dalszej nauce.