równania i nierównośni z wartością bezwzględną i parametrem Patricja: zbadaj liczbę rozwiązań równania ze względu na wartość parametru meR |x²−4x+3|=m zrobiłam to tak: f(x)=x²−4x+3 g(x)=m Δ=4 x1=1 x2=3 I narysowałam tego wykres i nie wiem jak odczytać z tego przypadki że dla 1 rozwiązania me(......)

wredulus_pospolitus: bierzesz linijke do ręki ustawiasz ją rownolegle do osi OX przesuwasz ją od dołu wykresu i sprawdzasz ... hmmm dla m=−10 linijka przecina mi się ... ...... razy wykres i tak przesuwasz linijkę aż do zmiany ilości 'przecięć' (styków) z funkcją f(x) rozumiemy

Patricja: nadal zbytnio nie rozumiem jak i tak, cały czas źle mi wychodzi i skad tam sie biora te rozwiazania a u mnie w odp. jest napisane ze 4 rozwiazania gdy me(0,1) a ja tego nie widze

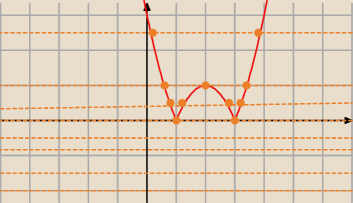
wredulus_pospolitus: masz linijkę ... lecisz nią 'od dolu' ukladu na początku w ogole Ci się nie przecina z wykresem ... czyli brak rozwiązań 'dochodzisz' do osi OX i ... ooo ... styk w dwoch miejscach ... czyli dla m=0 masz dwa rozwiązania (x=1 i x=3) i lecisz dalej i masz tu już cztery razy przecięcie aż dojdziesz do punktu gdzie będą tylko 3 przecięcia (styki) a powyżej już tylko dwa ... i tak już do końca tylko dwa będa zapisujesz to co zaobserwowalaś

wredulus_pospolitus: 'omskła' mi się raz 'linijka' i nie jest równoległa do osi OX

Patricja: Już mniej więcej zrozumiałam Dziekuję