ratujcie! PILNE Matylda: Trójkąt o bokach długości |AB|=6, |BC|=5, |AC|=5,5 jest podobny do trójkąta DEF. Wiedząc, że średni bok trójkąta DEF jest równy najmniejszemu dokowi trójkąta ABC, podaj ich skalę podobieństwa i oblicz obwód trójkąta DEF.

Matylda: pomocy

AROB: Pomogę

Matylda: o dzięki chodzi mi o ułożenie proporcji

Matylda: haloo?

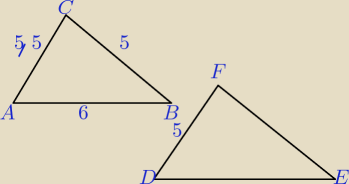
AROB: Bokowi średniej długości w ΔABC odpowiada dok średniej długości w ΔDEF. Zatem skalę podobieństwa obliczymy z ich stosunku:

	5,5
k =		= 1,1
	5

ΔABC ∼ ΔDEF, a stąd obliczymy pozostałe boki ΔDEF. IABI = k * IDEI IBCI = k * IEFI 6 = 1,1 * IDEI 5 = 1,1 * IEFI

	6		60		5		5		50		7
IDEI=		=		=5		IEFI=		=		=4
	1,1		11		11		1,1		11		11

Matylda: dzieki

AROB: Przepraszam, że tak długo musiałaś czekać, ale zostałam oderwana przez telefon.

Matylda: a da rade to zrobić ze zwykłej proporcji?

Matylda: nic nie szkodzi dziękuje za poświęcony czas. Próbowałąm zrobic to zadanie z proporcji boków ale wyniki wychodza kosmiczne

Matylda: zrobiłaś błąd bo w poleceniu jest że: ŚREDNI bok długości trójkąta DEF odpowiada NAJMNIEJSZEMU bokowi trójkąta ABC chyba ze to nic nie zmienia

AROB: Można też skorzystać z proporcji ( bo w trójkątach podobnych odpowiednie boki są proporcjonalne). Ale mając już znaną skalę, prościej jest właśnie tak. A proporcje byłyby takie:

	5,5		5		5,5		6
np.		=		i		=
	5		EF		5		DE

Powodzenia!

Matylda: ok dzieki juz wiem wszystko

AROB: Nie Matyldo, On nie odpowiada, tylko jest równy ( tak podałaś w treści). A z resztą nie jest możliwe, żeby średniemu bokowi odpowiadał najmniejszy, bo wtedy nie byłyby to trójkąty podobne.

Matylda: rozumiem dziekuje jeszcze raz