Niech O(O, r) będzie okręgiem o środku w pkt O i promieniur, a P dowolnym punkte
???: Niech O(O, r) będzie okręgiem o środku w pkt O i promieniu r, a P dowolnym punktem odległym od
środka okegu o d. Wykąż, że jeżeli PB jest sieczną przecinającą okrąg w pkt A i B to
|PA||PB|=|d2 − r2|
brak mi pomyslu na to zadanie.
20 lis 22:38
???: up
20 lis 23:04
Eta:
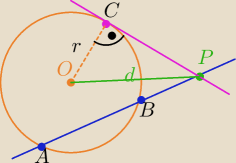
Z twierdzenia o stycznej i siecznej mamy:
|PA|*|PB|= |PC|
2 i z tw. Pitagorasa w trójkącie CPO |PC|
2= |d
2−r
2|
to: |PA|*|PB|= |d
2−r
2|
20 lis 23:24
Bizon:
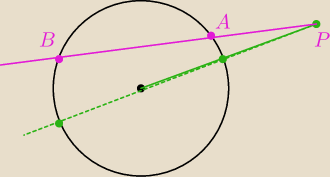
z twierdzenia o siecznych
|PA||PB|=(d−r)(d+r)
20 lis 23:32
 Z twierdzenia o stycznej i siecznej mamy:
|PA|*|PB|= |PC|2 i z tw. Pitagorasa w trójkącie CPO |PC|2= |d2−r2|
to: |PA|*|PB|= |d2−r2|
Z twierdzenia o stycznej i siecznej mamy:
|PA|*|PB|= |PC|2 i z tw. Pitagorasa w trójkącie CPO |PC|2= |d2−r2|
to: |PA|*|PB|= |d2−r2|
 z twierdzenia o siecznych
|PA||PB|=(d−r)(d+r)
z twierdzenia o siecznych
|PA||PB|=(d−r)(d+r)