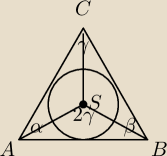
W trójkącie ABC mamy dane: |∠A|=20stopni |∠B|=60. Punkt S jest środkiem okręgu w kamczatka: W trójkącie ABC mamy dane: |∠A|=20stopni |∠B|=60. Punkt S jest środkiem okręgu wpisanego w ten trójkąt. Oblicz miary kątów ASB,BSC,ASC. α=20 β=60 więc γ=180−80=100 więc kąt ASB wynosi 200 stopni a w odpowiedziach mam że wynosi on 140 stopni czemu ?

kamczatka: ?

kamczatka: ?

Hajtowy: Podpowiedź: Środek okręgu wpisanego w trójkąt leży na przecięciu dwusiecznych.

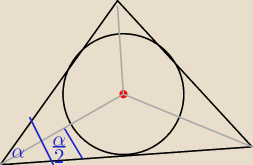
ktosia: żeby w trójkąt wpisać okrąg należy poprowadzić dwusieczne kątów, punkt s jest miejscem przecięcia się ich, więc do trójkąta abs uwzględniasz połowę kąta alfa=10, połowę beta=30 więc 180−10−30=140

ktosia: i analogicznie w reszcie

ktosia: a tym sposobem którym liczyłaś można postępować w przypadku gdy okrąg jest opisanyna trójkącie a nie wpisany

Hajtowy:

Piotr 10: Coś nie tak chyba

Hajtowy: Czemu nie tak?

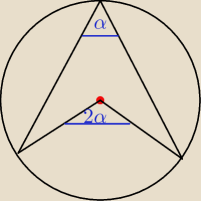
ktosia: tak jak narysowałeś to w przypadku gdy okrąg jest opisany a nie wpisany!

ktosia: miara kąta wpisanego w okrąg (a nie opisanego na nim) jest równa połowie miary kata rodkowego opisanego na tym samym łuku

ktosia: *środkowego

ktosia:

ktosia:

ktosia: w tym zadaniu chodzi o drugi rysunek

kamczatka: wielkie dzięki

ktosia:

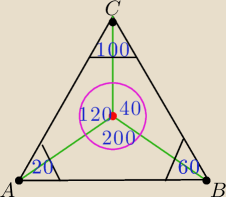
kamczatka: a czemu |∠BSC|=100 i |∠ASC|=120 ?

kamczatka: ASC to pewnie temu że 2*β=120 stopni ale skąd te to w kącie BSC powinno być podobnie 2*α

kamczatka: dobra już wiem γ=100 więc połowa równa się50