ekstrema Dar: Znajdź ekstremum a) f(x) = x√x−1* b) f(x) = x²√x²−4* c) f(x) = (x−7)²√x²+2* * Pierwiastki trzeciego stopnia. Problem w wyciągniętej dość skomplikowanej pochodnej i jej późniejszym przyrównaniu do 0. Bardzo proszę o pomoc!

wredulus_pospolitus: to pokaż jak Ci pochodna wyszła w takim razie

Dar: w a) (x−1)(do potęgi 1/3) + 1/3(x−1)(do potęgi −2/3) x w b) 2x(x²−4)(do potęgi 1/3) + x²(1/3(x²−4)(do potęgo − 2/3) I w tym miejscu stoję

Dar: Podbijam.Wie ktoś jak sprowadzić to do wspólnego mianownika?

Dar: podbijam. Bardzo proszę o szybką odp.!

AS: w a) proponuję wprowadzić x pod znak pierwiastka i szukać ekstremum wyrażenia podpierwiastkowego podobnie w b) wprowadzić x²

Basia: czy to ma być w (a) f(x) = x*³√x−1 = x*(x−1)^1/3 jeżeli tak to

	1
f'(x) = 1*(x−1)1/3 + x*		*(x−1)−2/3 =
	3

	x
3√(x−1) +		=
	33√(x−1)2

33√x−1*3√(x−1)2 + x
	=
33√(x−1)2

33√(x−1)3+x		3(x−1)+x
	=		=
33√(x−1)2		33√(x−1)2

5x−1
33√(x−1)2

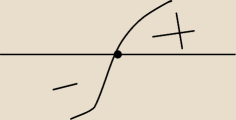
As: pod koniec będziemy przyrównywać mianownik do zera, czyli 4x−3=0 4x=3 x=3/4 −−> punkt stacjonarny Współczynnik 4x jest dodatni, więc funkcja ma minimum w punkcie x=3/4(bo w sąsiedztwie punktu 3/4 zmienia znak z "−" na "+".