Zespolone - wzór de Moivre'a
Beata: Proszę o pomoc
Korzystając ze wzoru de Moivre'a obliczyć :
( 1−i)11 =
20 lis 11:14
Janek191:
z = 1 − i
I z I =
√11 +(−1) =
√1 + 1 =
√2
| | a | | 1 | | √2 | |
cos φ = |
| = |
| = |
| |
| | I z I | | √2 | | 2 | |
| | b | | − 1 | | √2 | |
sin φ = |
| = |
| = − |
| |
| | I z I | | √2 | | 2 | |
zatem
z = 1 − i =
√2*( cos 270
o + i sin 270
o)
Teraz wstawiamy do wzoru :
z
n = I z I
2 * ( cos n φ + i sin n φ )
z
11 = (
√2)
11 *( cos 11*270
o + i sin 11*270
o) =
= 32
√2*( cos 2 970
o + i sin 2 970
o )
= 32
√2*( cos ( 8*360 + 90)
o + i sin ( 8* 360 + 90)
o) =
= 32
√2*( cos 90
o + i sin 90
o) = 32
√2*( 0 + i ) = 32
√2 i
===============================================
20 lis 11:48
Janek191:
z = 1 − i
I z I =
√11 +(−1) =
√1 + 1 =
√2
| | a | | 1 | | √2 | |
cos φ = |
| = |
| = |
| |
| | I z I | | √2 | | 2 | |
| | b | | − 1 | | √2 | |
sin φ = |
| = |
| = − |
| |
| | I z I | | √2 | | 2 | |
zatem
z = 1 − i =
√2*( cos 270
o + i sin 270
o)
Teraz wstawiamy do wzoru :
z
n = I z I
2 * ( cos n φ + i sin n φ )
z
11 = (
√2)
11 *( cos 11*270
o + i sin 11*270
o) =
= 32
√2*( cos 2 970
o + i sin 2 970
o )
= 32
√2*( cos ( 8*360 + 90)
o + i sin ( 8* 360 + 90)
o) =
= 32
√2*( cos 90
o + i sin 90
o) = 32
√2*( 0 + i ) = 32
√2 i
===============================================
20 lis 11:48
Janek191:
Pomyłka !
W II wierszu powinno być :
I z I =
√12 + (−1)2 =
√2
20 lis 11:51
Janek191:
We wzorze Moivre'a zamiast 2 powinno być n
20 lis 11:53
Beata: mógłbyś mi jeszcze podpowiedzieć jak obliczasz φ ? że 270 ?
20 lis 12:00
pigor: ... możesz szybciej np. z tangensa : tgφ=
ba= −1 ⇒ φ= − 45
o= −
14π
a stąd łatwo masz sinφ i cosφ . ...
20 lis 12:10
Janek191:
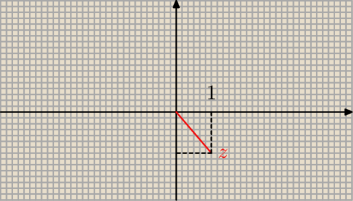
Pomyliłem się, powinno być 315
o = − 45
o
20 lis 12:15
Janek191:
cos 11*315
o = cos 3 465 = cos ( 9*360 + 225)
o = cos 225
o =
| | √2 | |
= cos ( 180 + 45)o = − cos 45o = − |
| |
| | 2 | |
| | √2 | |
sin 11*315o = sin 225o = sin (180 + 45)o = − sin 45o = − |
| |
| | 2 | |
Odp.
| | √2 | | √2 | |
z11 = 32√2*( − |
| − |
| i ) = − 32 − 32 i |
| | 2 | | 2 | |
20 lis 12:23