. Piotr 10: Tworzymy wszystkie liczby siedmiocyfrowe o cyfrach należących do zbioru {1;2;3;4;5;6}. Cyfry w liczbie mogą się powtarzać.Ile jest takich liczb, w których: a) cyfry 3 i 4 sąsiadują ze sobą a pozostałe cyfry są większe od 4; b) cztery cyfry są równe 5 i pozostałe trzy cyfry różnią się między sobą; c) co najmniej dwie cyfry są nie mniejsze niż 4 ? Proszę o pomoc

Piotr 10:

	7 2
a)		=21

21*2*2=84 Ale to źle

Mila: Jakie propozycje?

Piotr 10: Myślę, ale ciężko ciężko

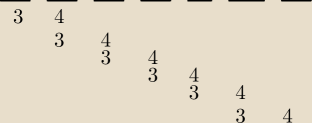
Saizou : wiemy że liczby 4 i 3 muszą stać obok siebie , czyli mamy 6 opcji rozmieszczenia, możemy te liczby przemieszać tworząc 34 lub 43 czyli będziemy mnożyć razy 2!, no i jeszcze trzeba dopełnić liczbę aby miała 7 cyfr i muszą być one większe od 4 czyli 5,6, zatem 2⁵ ostatecznie mamy 6*2!*2⁵ tak mi się wydaje

Mila: A) podpowiedź, zestaw (3,4) traktuj jak jeden element.

Piotr 10: wynik się zgadza, kurde a zaczynałem tak jak Ty, też 2!*6 a potem doszedlem do wniosku, że to źle

Mila: Saizou,

Piotr 10: Robiłem tak samo jak Saizou, lecz doszedłem do wniosku po przeczytaniu ''Cyfry mogą się powtarzać'', że będzie inaczej eh

Mila: Dalej, (b) i (c) BEZENDU?

Piotr 10: Próbuje zrobić

Hajtowy: b) 5 5 5 5 L L L L 5 5 5 5 L L L L 5 5 5 5 L L L L 5 5 5 5 Ustawiliśmy je na 4 sposoby Pozostałe liczby możemy ustawić na 5*4*3 sposoby Odpowiedz jak brzmi?

Piotr 10: b) 2100 c) 262 440 Proszę na razie nie wstawiać rozwiązań

Hajtowy: Piotr 10, pytam się Ciebie Jak wg Ciebie brzmi rozwiązanie tego co Ci napisałem

Piotr 10: Nie wiem, nie znam się za bardzo

Hajtowy: Tfu... źle Ci to zrobiłem Ale wiem już jak Jak dojdziesz do tego to powiedz... Mała podpowiedź.

	coś coś
Wybierasz 4 miejsca na cyfrę 5, czyli		⇒pomyśl

A na pozostałe: pierwszą na 5 drugą na 4, trzecią na 3 sposoby

Hajtowy: c) proponuję zdarzenie przeciwne zrobić. będzie szybciej i wygodniej

Piotr 10: b)

7 4
	=35

Na tyle sposobów mogę rozmieścić cztery cyfry, które są równe 5 potem 5*4*3=60 60*35=2100 Wyszło

Mila: Pięknie. Ostatni punkt trudny, chyba że PW wymyśli łatwy sposób.

Piotr 10: Myślę, zdarzenie przeciwne trzeba zrobić W^k_n=n^k=279936 i teraz coś odjąć

Piotr 10: Mila wyszło mi, nie wiem jak ale wyszło

Hajtowy: Wymyśliłem coś dla Ciebie ciekawego Nie jest to rozwiązanie zadania dosłowne, lecz częściowe. Teraz musisz ostro nad tym pomyśleć a^y − ilość wszystkich liczb siedmiocyfrowych z cyfr {1, 2, 3, 4, 5, 6} A'− 0 cyfr większych lub równych 4, lub 1 cyfra większa lub równa 4 x^y − liczby z cyfr {1,2,3}

coś1 coś1
	= ... wybieram miejsce dla liczby większej lub równej 4

coś2 coś2
	= ... wybieram jedną ze zbioru {4,5,6}

x^z − na pozostałe miejsca ze zbioru{1,2,3} |A'| = ...

	coś1 coś1		coś2 coś2
A = ay − (xy +		*		* xz)

Piotr 10: Hajtowy zrobiłem

Hajtowy: Gratuluję

Piotr 10: Dzięki