przeksztalcenia zadanie: Przeksztalcenie liniowe T zadane jest wzorem: 1) x'=−2x+y, y'=−x−y 2) T(x, y)=(2x−3y, −2x) a) znajdz obrazy wersorow przez przeksztalcenie T b) napisz macierz przeksztalcenia T c) Znajdz rownania prostych ktore sa obrazami osi ukladu wspolrzednych przez przeksztalcenia T. Zrob to dwoma sposobami: poslugujac sie rownaniami ogolnymi oraz rownaniem parametrycznym. 1)x'=−2x+y y'=−x−y a) e₁=(−2,−1); e₂=(1,−1) b) m(T)= −2 1 −1 −1 c) os OX czyli (x, 0), os OY czyli (0, y) a dalej co do czego podstawic? 2) T(x, y)=(2x−3y, −2x) x'=2x−3y y'=−2x a) e₁(2,−2); e₂(−3,0) b) m(T)= 2 −3 −2 0 c) poprosilbym o sprawdzenie a) i b) i pomoc w c)

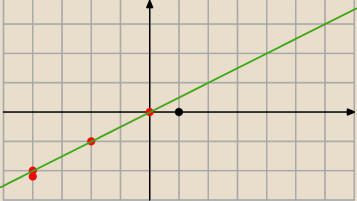
Mila: c) Oś OX: y=0 równanie ogólne bo masz 0*x+y=0 Oś Oy: x+0y=0⇔x=0 równanie ogólne x'=−2x+y⇔x'−y=−2x

	x'+y'
y'=−x−y⇔y'+x=−y podstawiam do pierwszego: x'+y'+x=−2x⇔x'+y'=−3x, x=
	−3

	−1		1
x=		x'−		y'
	3		3

do drugiego

	−1		1
y'+		x'−		y'=−y
	3		3

	1		2
y=		x'−		y'
	3		3

	1		2
Oś OX: y=0 po przekształceniu:		x'−		y'=0⇔x'−2y'=0⇔x−2y=0
	3		3

Sprawdź na dwóch punktach osi (0,0), (1,0) obrazem prostej jest prosta, bo to jest przekształcenie afiniczne, dalej sam, po kolacji więcej.

zadanie: dziekuje wroce do tego jutro bo teraz juz ide spac

Mila: dobranoc.

zadanie: os OY: x=0

	1		1
−		x'−		y'=x
	3		3

	1		1
−		x'−		y'=0 /*3
	3		3

−x'−y'=0 x+y=0 dobrze?

Mila: Tak.

zadanie: a parametrycznie? os OX: y=0 punkt nalezacy do tej prostej to (x, 0) i wektor rownolegly do tej prostej [1, 0] rownanie parametryczne: x'=x+t→x=x'−t y'=0 czyli: wstawiam do przeksztalcenia: x'=−2(x'−t)+0=−2x'+2t y'=−(x'−t)−0=−x'+t dobrze?

zadanie: ?

zadanie:

	2
Przeksztalcenie afiniczne zadane jest wzorem T(x, y)=(3x+4y+1, 4x−3y−		)
	3

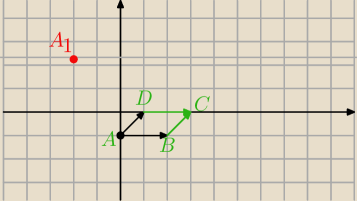
a) znajdz obrazy wersorow osiowych przez to przeksztalcenie. b) dany jest pewien kwadrat o boku a. Jakie jest pole obrazu tego kwadratu przez przeksztalcenie T.c) Jakie figury sa obrazami rownolegloboku R zbudowanego na wektorach [1,1] i [2, 0] zaczepionych w punkcie (0,−1) pod wplywem tego przeksztalcenia. (rownanie parametryczne rownolegloboku). a) wersory osiowe to chyba wersory jedostkowe e₁=[1, 0]; e₂=[0, 1] e₁': x'=4 e₂': x'=5

	10		11
y'=		y'=−
	3		3

b) P(K)=a² P(L(K))=Idet(3 4 I *P(K)=25a² 4 −3) c) czy to obowiazuje rowniez do przeksztalcenia afinicznego? zaloze, ze tak v=[1,1] w=[2,0] A(0,−1) A+tv+sw ; t,s ∊ [0,1] (x, y)=(0, −1)+t[1,1]+s[2,0]=(t+2s, −1+t) podstawiam do przeksztalcenia T: x'=3(t+2s)+4(−1+t)+1=3t+6s−4+4t+1=7t+6s−3

	2		2		7
y'=4(t+2s)−3(−1+t)−		=4t+8s+3−3t−		=t+8s+
	3		3		3

	7
T(x, y)=(−3,		)+t[7,1]+s[6, 8]
	3

sprawdzam rownoleglosc wektorow [7,1] i [6, 8] (jesli sa rownolegle to obrazem bedzie punkt lub odcinek a jezeli nie to rownoleglobok) det(7 6 =56−6=50≠0 liniowo niezalezne czyli obrazem jest rownoleglobok 1 8) moglbym prosic o sprawdzenie tych zadan?

Mila: Pytanie , czy to przekształcenie zachowuje prostopadłość prostych, czy obrazem kwadratu jest kwadrat.

zadanie: rownoleglobok

zadanie: ale tam jest wyznacznik przy obliczaniu pola

Mila: Zauważyłam. Dobranoc

zadanie: ale dobrze zrobilem te trzy podpunkty?

zadanie: ?

Mila: Miałam nadzieję,że ktoś Ci odpowie. Poczytam, to odpowiem, w tej chwili wydaje mi się, że dobrze. Liczyłam.

Mila: Zgadza się.

zadanie: dziekuje bardzo