zadanie
Anika: znajdż wariancję i odchylenie standardowe następujących liczb,4,8,7,1,5,5,4,1
19 lis 15:50
M:
26 lis 06:00
Mariusz: Kroki obliczeń
1. Obliczenie średniej arytmetycznej
Średnia arytmetyczna (
𝑥
ˉ
x
ˉ
) to suma wszystkich liczb podzielona przez ich liczbę:
𝑥
ˉ
=
suma wszystkich liczb
liczba liczb
x
ˉ
=
liczba liczb
suma wszystkich liczb
Dla danych
4
,
8
,
7
,
1
,
5
,
5
,
4
,
1
4,8,7,1,5,5,4,1:
𝑥
ˉ
=
4
+
8
+
7
+
1
+
5
+
5
+
4
+
1
8
=
35
8
=
4.375
x
ˉ
=
8
4+8+7+1+5+5+4+1
=
8
35
=4.375
2. Obliczenie odchyleń od średniej
Każdą wartość odejmujemy od średniej (
𝑥
−
𝑥
ˉ
x−
x
ˉ
), a następnie podnosimy do kwadratu:
(
4
−
4.375
)
2
=
0.140625
,
(
8
−
4.375
)
2
=
13.140625
,
(
7
−
4.375
)
2
=
6.890625
(4−4.375)
2
=0.140625,(8−4.375)
2
=13.140625,(7−4.375)
2
=6.890625
(
1
−
4.375
)
2
=
11.390625
,
(
5
−
4.375
)
2
=
0.390625
,
(
5
−
4.375
)
2
=
0.390625
(1−4.375)
2
=11.390625,(5−4.375)
2
=0.390625,(5−4.375)
2
=0.390625
(
4
−
4.375
)
2
=
0.140625
,
(
1
−
4.375
)
2
=
11.390625
(4−4.375)
2
=0.140625,(1−4.375)
2
=11.390625
3. Obliczenie wariancji
Wariancja to średnia z tych kwadratów:
Wariancja
=
suma kwadrat
o
ˊ
w odchyle
n
ˊ
liczba liczb
Wariancja=
liczba liczb
suma kwadrat
o
ˊ
w odchyle
n
ˊ
Suma kwadrat
o
ˊ
w odchyle
n
ˊ
=
0.140625
+
13.140625
+
6.890625
+
11.390625
+
0.390625
+
0.390625
+
0.140625
+
11.390625
=
43.875
Suma kwadrat
o
ˊ
w odchyle
n
ˊ
=0.140625+13.140625+6.890625+11.390625+0.390625+0.390625+0.140625+11.390625=43.875
Wariancja
=
43.875
8
=
5.484375
Wariancja=
8
43.875
=5.484375
4. Obliczenie odchylenia standardowego
Odchylenie standardowe to pierwiastek kwadratowy z wariancji:
Odchylenie standardowe
=
5.484375
≈
2.341874
Odchylenie standardowe=
5.484375
≈2.341874
26 lis 11:14
frycz:
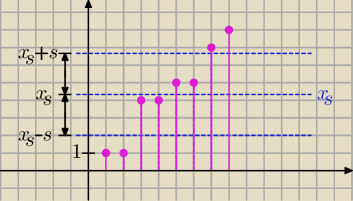
| | 1*2 + 4*2 + 5*2 + 7 + 8 | | 35 | |
średnia xs = |
| = |
| |
| | 8 | | 8 | |
wariancja
| | 1 | | 35 | | 35 | | 35 | | 35 | | 35 | |
s2= |
| * [2( |
| −1)2+2( |
| −4)2+2( |
| −5)2+( |
| −7)2+2( |
| −8)2)] |
| | 8 | | 8 | | 8 | | 8 | | 8 | | 8 | |
odchylenie standardowe = s
26 lis 15:36
