Suma miar dwóch kątów trójkąta jest równa α, a boki zawarte w ramionach trzecieg kamczatka: Suma miar dwóch kątów trójkąta jest równa α, a boki zawarte w ramionach trzeciego kąta mają długości a i b. Oblicz pole tego trójkąta. Czy mógłby ktoś zrobić do tego zadania rysunek ? Dzięki wielkie.

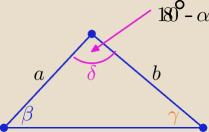
Eta: β+ γ=α to δ= 180^o−α

	1		1
P=		*a*b*sinδ=....... =		a*b*sinα
	2		2

kamczatka: czemu sinδ to sinα ?

kamczatka: w ogóle czemu sinδ=180−α to nie jest rozmiar kąta ?

krystek: Przeczytaj uważnie treść i zapis ETy δ=180−(β+γ)=180−α

kamczatka: tak wiem ale przecież to są miary kątów a nie sinus kąta

krystek: sinδ=sin(180−α)=sinα Wzory redukyjne.

kamczatka: aha to już wiem czemu sinα=sinδ ale czemu 180−α=sinδ ? Jak to przecież miara kąta

kamczatka: ?

krystek: A gdzie masz tak zapisane ,że sinδ=180−α

kamczatka: dobra już czaję dzięki.