protopadłość i równoległość Asia: Punkty A(−1,3) i C(5,5) sa wierzchołkami prostokąta ABCD, którego jeden z boków zawarty jest w prostej o równianiu y=x+4. Znajdź współrzędne wierzchołków B i D.

Asia: prosze o pomoc..

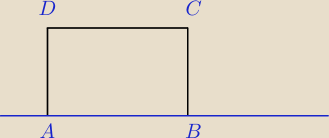
Janek191: A = ( − 1; 3) C = (5; 5) y = x + 4 Niech bok AB będzie zawarty w prostej o równaniu y = x + 4, więc B = ( x ; x + 4) Mamy → BA = [ − 1 − x; 3 − ( x + 4) ] = [ − 1 − x ; − x − 1 ] → BC = [ 5 − x ; 5 − ( x + 4) ] = [ 5 − x ; 1 − x ] Wektory → → BA i BC są prostopadłe, więc ich iloczyn skalarny jest równy 0 → → BA o BC = [ −1 − x ; − x − 1] o [5 − x ;1 − x ] = − (1 + x)*( 5 − x) + [ −( x + 1)]*(1 − x) = = − 5 + x − 5x + x² − x + x² − 1 + x = 2 x² − 4 x − 6 = 0 2 x² − 4 x − 6 = 0 / : 2 x² − 2 x − 3 = 0 Δ = (−2)² − 4*1*(−3) = 4 + 12 = 16 √Δ = 4 więc

	2 − 4		2 + 4
x =		= − 1 lub x =		= 3
	2		2

y = − 1 + 4 = 3 lub y = 3 + 4 = 7 zatem B = ( − 1 ; 3) = A − odpada lub B = ( 3; 7 ) ===================================== Mamy → → AB = DC A = ( − 1; 3), B = ( 3; 7 ) → AB = [ 3 − (−1) ; 7 − 3 ] = [ 4 ; 4 ] C = ( 5; 5) D = ( x ; y ) → DC = [ 5 − x ; 5 − y ] więc 4 = 5 − x i 4 = 5 − y x = 1 i y = 1 D = ( 1 ; 1) =========

pigor: ... , Punkty A(−1,3) i C(5,5) sa wierzchołkami prostokąta ABCD, którego jeden z boków zawarty jest w prostej o równaniu y= x+4. Znajdź współrzędne wierzchołków B i D. −−−−−−−−−−−−−−−−−− lub bez wektorów i ich iloczynu skalarnego np. tak : A=(−1,3) ∊ k: y=x+4 , a C=(5,5)∉ k , no to niech B=(x,x+4) , to prosta CB taka, że CB⊥k : x−y+4=0 ⇒ CB: 1(x−5)+1(y−5)=0 ⇔ CB : x+y=10 i k : x−y= −4 ⇔ ⇔ 2x= 6 i y=x+4 ⇔ (x,y)= (3,7) =B − szukany wierzchołek ; dalej, ponieważ środek AC: S= (¹₂*4, ¹₂*8)= (2,4) jest zarazem środkiem DB, gdzie D=(x,y) i B=(3,7) ⇒ x+3=2*2 i y+7= 2*4 ⇔ (x,y)= (1,1) =D − szukany wierzchołek prostokąta ABCD . ...